转自:http://lib.csdn.net/article/architecture/5384
摘要:本部分首先简单介绍 sharding 系统的基本架构,然后重点介绍 sharding 机制中常用的三种表数据划分方法。
一. 数据划分算法
1. Sharding 系统的基本结构
上节我们说到 Sharding 可以简单定义为将大数据库分布到多个物理节点上的一个分区方案。每个 shard 都被放置在一个节点上面。Sharding 系统是一个 shared-nothing 的系统,基本上都采用下图中所示的架构。最下面是很多数据库服务器节点,每个节点上面都会运行一个或多个数据库的实例。中间一层叫做查询路由器,客户端的连接都通过它进行转发。查询路由器负责解析用户的查询语句,并将这些语句转发到包含有所需要的数据的 shard 节点上面去执行。执行的结果也会通过查询路由器进行汇总并发送给相应的客户端。
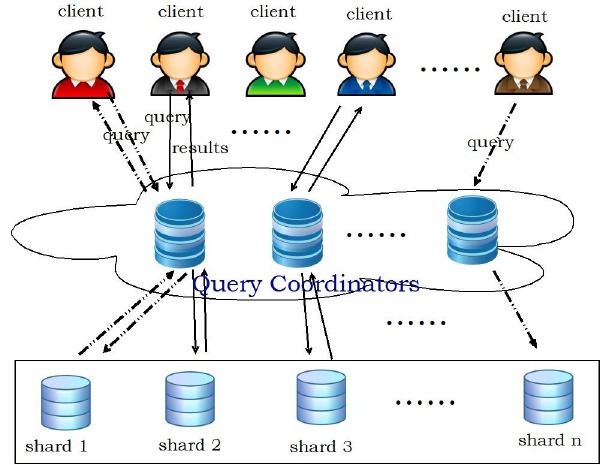
对于这样一个 sharding 系统,我们需要考虑到下面几个问题:如何将数据划分到多个 shard 节点上面;用户的查询语句如何正确的转发到相应的节点上面去执行;当节点数据变化的时候怎样重新划分数据。对于数据划分和查询路由来说,所用的算法一般是对应的。下面就讲一下一些常用的数据划分的方法。这里的假设前提是:只考虑单个表,并且这个表的划分键(Partitioning Key)已经被指定。
2. 常见的表划分算法
本节介绍三种常见的数据划分方法:轮流放置(Round-Robin)、一致性哈希(Consistent Hashing)和区间划分(Range-based Partitioning)。
2.1 Round-Robin
轮流放置是最简单的划分方法:即每条元组都会被依次放置在下一个节点上,以此进行循环。一般在实际应用中为了处理的方便,通常按照主键的值来决定次序从而进行划分。即给定一个表T,表T的划分键(Partitioning Key)是 k,需要划分的节点数目 N,那么元组 $t ∈ T$ 将会被放置在节点 n 上面,其中 $n = t.k mod N$。由于划分只与划分键有关,因此我们可以把对元组的划分简化为对数字的划分,对于不是数字的键值可以通过其它方式比如哈希转化为数字形式。下面给出一个例子来表示这种划分方式,把 9 个元组分布到 3 个节点上的情况。
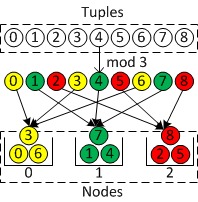
但是,简单的直接用划分键上的值来计算放置节点的算法可能会造成数据的不均匀。因此,轮流放置有很多改进版,比如说哈希方式(Hashing),即 $n = hash(t.k) mod N$。先将划分键的值进行 hash 操作,变成一个与输入分布无关、输出均匀的值,然后再进行取模操作。哈希函数可以有很多选择,你可以针对你的应用的特征去选取。
Pros: 轮流放置算法的实现非常简单,而且几乎不需要元数据就可以进行查询的路由,因此有着比较广泛的应用。例如 EMC 的 Greenplum 的分布式数据仓库采用的就是轮流放置和哈希相结合的方式。
Cons: 轮流放置同样具有很明显的缺点:当系统中添加或者删除节点时,数据的迁移量非常巨大。举个有 20 个节点的例子(下表),当系统由 4 个节点变为 5 个节点时,会有如下的放置结果:红色部分是 $mod 4$ 和 $mod 5$ 时结果不相等的情况,不相等意味着这些元组当系统由 4 个节点变为 5 个节点时需要进行迁移。也就是说多达 80% 的元组都需要迁移。数据的迁移会对系统的性能造成很大的影响,严重时可能会中断系统的服务。当系统的节点数目频繁变化时,是不提倡使用这种方式的。

数据迁移量大的问题可以通过改进轮流放置算法来达到,比较常见的两个改进算法是一致性哈希和分区划分算法。
2.2 Consistent Hashing
一致性哈希是一种特殊的哈希方式。传统的哈希方式(在上一小节中讲到)在当节点数目发生变化时,会引起大量的数据迁移。而使用一致性哈希则不会产生这种问题。一致性哈希最早是一个分布式缓存(Distributed Caching)系统的放置算法(现在很热门的Memcached就用的是一致性哈希)。但是现在它已经被广泛应用到了其它各个领域。对于任何一个哈希函数,其输出值都有一个取值范围,我们可以将这个取值区间画成一个环,如下图所示:
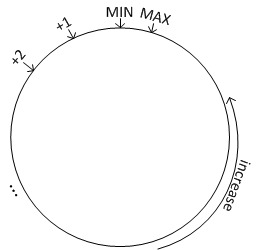
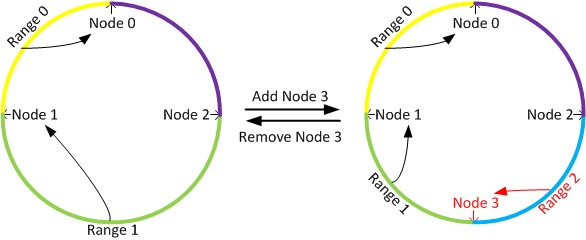
通过哈希函数,每个节点都会被分配到环上的一个位置,每个键值也会被映射到环上的一个位置。这个键值最终被放置在距离该它的位置最近的,且位置编号大于等于该值的节点上面,即放置到顺时针的下一个节点上面。下图形象的表示了这种放置方案,其中 Node 0 上面放置 Range 0 上面的数据,以此类推。
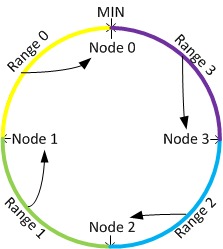
Pros: 由于采用的哈希函数通常是与输入无关的均匀函数,因此当键值和节点都非常的多的时候,一致性哈希可以达到很好的分布式均匀性。并且由于特殊的放置规则,一致性哈希在节点数据发生变动时可以将影响控制在局部区间内,从而保证非常少的数据迁移(接近理论上的最小值)。当增加一个节点时,只有这个节点所在的区间内的数据需要被重新划分,如下图中,只需要将 range 2 上面的数据会从 node 1 中迁移到 node 3 上面。当删除一个节点时,只需要将这个节点上面的数据迁移到下一个节点上面,比如删除 node 3,只把 range 2 上面的数据迁移到 node 1 上面就可以并,而其它的数据是不需要迁移变动的。
一致性哈希有非常广泛的应用,Key-Value 系统,文档数据库或者分布式关系数据库都可以使用。Amazon 的 NoSQL 系统 Dynamo 应用采用的就是一种改进的一致性哈希算法。在这个系统中又引入了虚拟节点的概念,使得这个算法的 load balance 更加的好,并且同时考虑了复制技术。环上的点就变成了虚拟节点,然后再采用其它的方式将这些虚拟节点映射到实际的物理节点上面去。这使得系统有很好的可扩展性和可用性。
2.3 Range-Based Partitioning
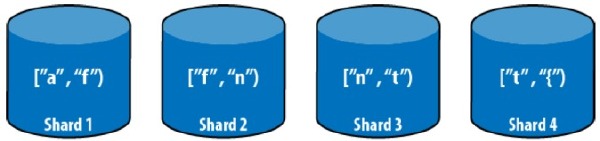
区间划分是现在很热门的 NoSQL 数据库 MongoDB 的 sharding 方案中所使用的算法。系统会首先把所有的数据划分为多个区间,然后再将这些区间分配到系统的各个节点上面。最简单的区间划分是一个节点只持有一个区间:在有 n 个节点的情况下,将划分键的取值区间均匀划分(这里的均匀是指划分后的每个 partition 的数据量尽量一样大,而并非值域区间一样大)为 n 份,然后每个节点持有一块。例如,按照用户名首字母进行划分,可能有以下的划分方案:
如果发生数据分布不均匀的情况,可以通过调整区间分布达到均匀情况,数据迁移同样会很小。
但是另外一些情况下,可能会导致连锁迁移。
- 情况一:数据分布不均,调整导致的连锁迁移
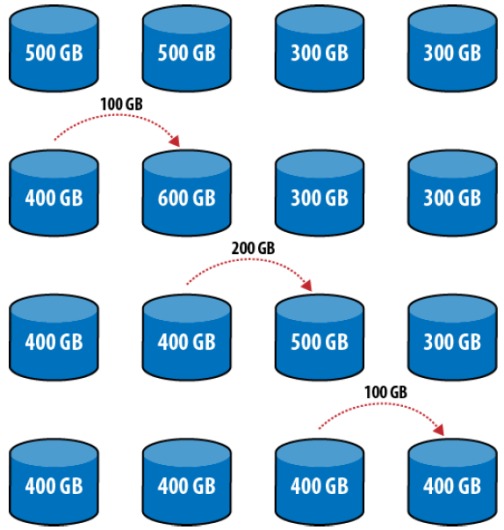
- 情况二:增加或删除节点导致的连锁迁移:
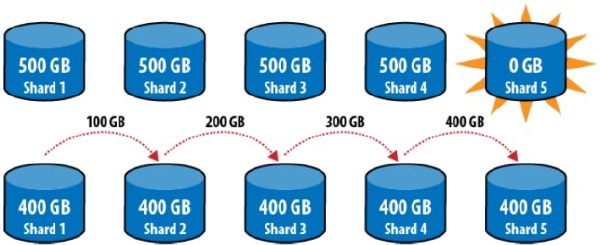
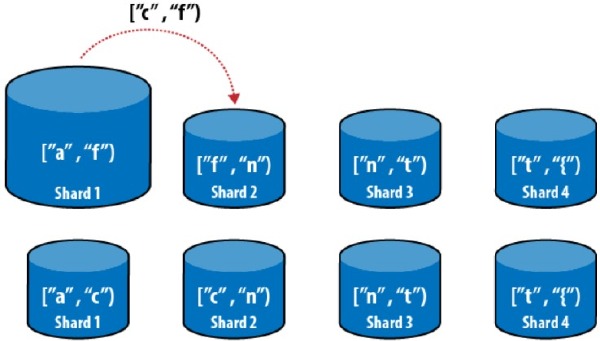
为了解决这个问题,MongoDB 采用的是每个节点持有多个区间的方案(Multiple range shards)。当需要进行迁移的时候,将持有过多数据的节点上的区间分裂,使得分裂出来的区间刚好满足迁移需要,然后再进行迁移。举例来说(下图),如果 shard 中存有 $[a, f]$ 区间的数据,数据量为 500G,此时需要从 shard 1 上面迁移 100G 到 shard 4,以保证数据的均匀分布。经统计,shard 1 中的 $[a, d]$ 段的数据为 400G,$[d, f]$ 段数据为 100G,因此将 shard 1中的 $[d, f]$ 段的数据直接迁移到 shard 4 上面。同理,需要从 shard 2 中迁移 100G 的数据到 shard 3 中。这种迁移方式的数据迁移量是理论上的最小值。
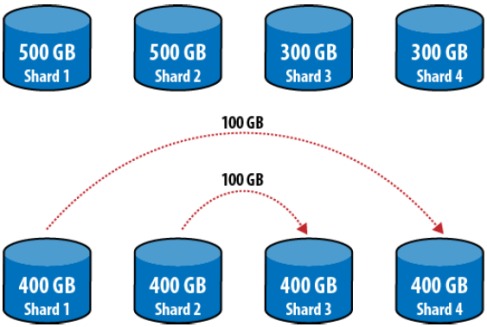
Cons: 每个节点多个区间的做法的缺点是使得对元数据的处理变得复杂,我们需要记录每个节点上面存储的所有区间。但是一般来说,每个节点上面的区间数目不是很大,因此元数据的数目不会很大。这种同时保证了数据的最小迁移,并且实现也比较简单的方案是一个很理想的做法,虽然它的无数据管理和同步上面会有一些问题。
另外,区间划分非常适合处理有区间查询的查询语句,但是也带来很大的一个 trade-off。如果一个查询需要访问到多条元组,那么对区间的边界的选取就变得非常棘手,如果选择不当的话,很容易造成一个查询需要在多个节点上面进行运行的情况,这种跨节点的操作会对系统的性能进行很大的影响。