感知机（perceptron）是二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取 +1 和 -1 二值。感知机对应于输入空间（特征空间）中将实例划分为正负两类的分离超平面，属于判别模型。
感知机模型
由输入空间到输出空间的如下函数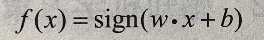 
称为感知机。其中，w 和 b 为感知机模型参数， w 叫作权值（weight）或权值向量（weight vector），b 叫作偏置（bias）。sign 是符号函数，即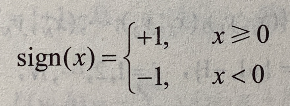 
感知机学习策略
数据集的线性可分性
如果存在某个超平面 S 能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧，则称数据集 T 为线性可分数据集（linearly separable data set）；否则，称数据集 T 线性不可分。
感知机学习策略
感知机的损失函数定义为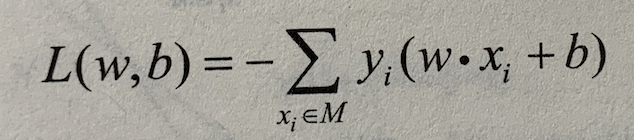 
其中 M 为误分类点的集合。这个损失函数就是感知机学习的经验风险函数。
显然，损失函数 L(w, b) 是非负的。如果没有误分类点，损失函数值是 0.而且，误分类点越少，误分类点离超平面越近，损失函数值越小。
感知机学习的策略是在假设空间中选取使损失函数式最小的模型参数 w 和 b，即感知机模型。
感知机学习算法
感知机学习问题转化为求解损失函数式的最优化问题，最优化的方法是随机梯度下降法。
感知机学习算法的原始形式
这种学习算法直观上有如下解释：当一个实例点被误分类，即位于分离超平面的错误一侧时，则调整 w, b 的值，使分离超平面向该误分类点的一侧移动，以减小该误分离点与超平面间的距离，直至超平面越过该误分类点使其被正确分类。
算法的收敛性
感知机学习算法的对偶形式
实例点更新次数越多，意味着它距离分离超平面越近，也就越难正确分类（越容易分错，超平面一动不多就容易将这些点分错），换句话说，这样的实例对学习结果影响最大（在支持向量机中，这些点代表着支持向量）。
