统计学系方法-第6章-逻辑斯谛回归与最大熵模型

逻辑斯谛回归（logistic regression）是统计学习中的经典分类方法。最大熵是概率模型学习的一个准则，将其推广到分类问题得到最大熵模型（maximum entropy model）。逻辑斯蒂回归模型与最大熵模型都属于对数线性模型。

逻辑斯谛回归模型

逻辑斯谛分布

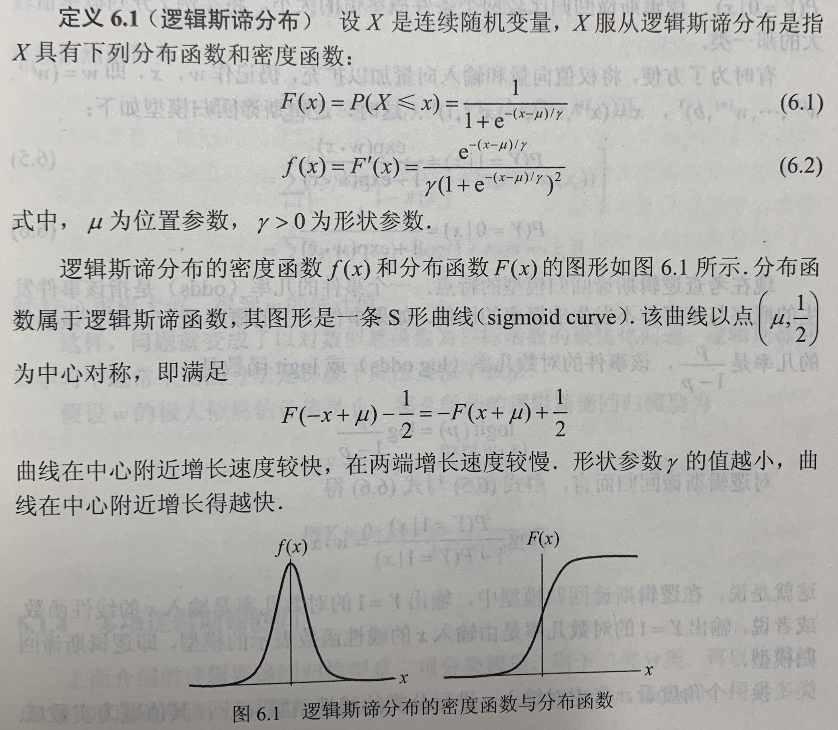
二项逻辑斯谛回归模型

二项逻辑斯谛回归模型（binomial logistic regression model）是一种分类模型，由条件概率分布 P(Y|X) 表示，形式为参数化的逻辑斯谛分布。这里，随机变量 X 取值为实数，随机变量 Y 取值为 1 或 0。

一个事件的几率（odds）是指该事件发生的概率与该事件不发生的概率的比值。如果事件发生的概率是 p，那么该事件的几率是 p/(1-p)，该事件的对数几率（log odds）或 logit 函数是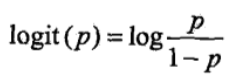

对逻辑斯谛回归而言，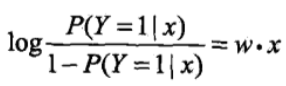

这就是说，在逻辑斯谛回归模型中，输出 Y=1 的对数几率是输入 x 的线性函数。或者说，输出 Y=1 的对数几率是由输入 x 的线性函数表示的模型，即逻辑斯谛回归模型。

模型参数估计

多项逻辑斯谛回归

最大熵模型

最大熵模型（maximum entropy model）由最大熵原理推导实现。

最大熵原理

最大熵原理是概率模型学习的一个准则。最大熵原理认为，学习概率模型时，在所有可能的概率模型（分布）中，熵最大的模型是最好的模型。通常用约束条件来确定概率模型的集合，所以，最大熵原理也可以表述为在满足条件的模型集合中选取熵最大的模型。

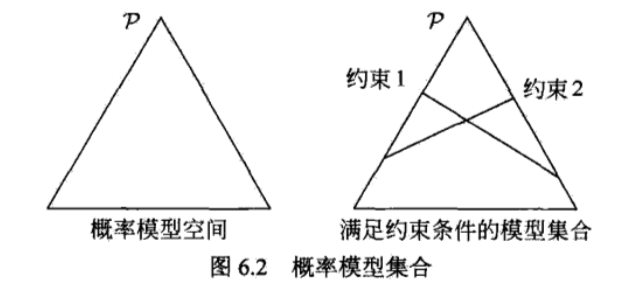
最大熵模型的定义

最大熵模型的学习

最大熵模型的学习过程就是求解最大熵模型的过程。最大熵模型的学习可以形式化为约束最优化问题。

求解上述约束最优问题，所得出的解，就是最大熵模型学习的解。

将约束最优化的原始问题转换为无约束最优化的对偶问题。通过求解对偶问题求解原始问题。

由于拉格朗日函数 L(P, w) 是 P 的凸函数，原始问题（6.18）的解与对偶问题（6.19）的解是等价的。

极大似然估计

模型学习的最优化算法

逻辑斯谛回归模型、最大熵模型学习归结为似然函数为目标函数的最优化问题，通常通过迭代算法求解。从最优化的观点看，这时的目标函数具有很好的性质。它是光滑的凸函数，因此多种最优化的方法都适用，保证能找到全局最优解。常用的方法有改进的迭代尺度法、梯度下降法、牛顿法或拟牛顿法。牛顿法或拟牛顿法一般收敛速度更快。