转自：https://www.matongxue.com/madocs/939.html
与原点的最短距离
假如有方程：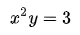
图像是这个样子滴：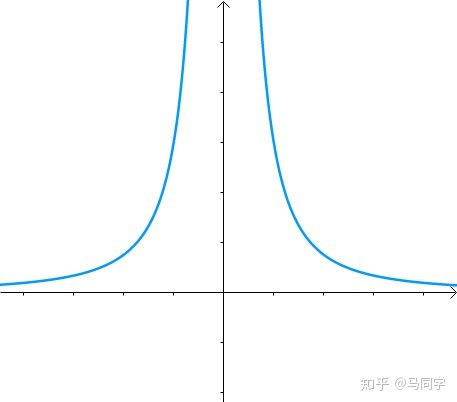
现在我们想求其上的点与原点的最短距离：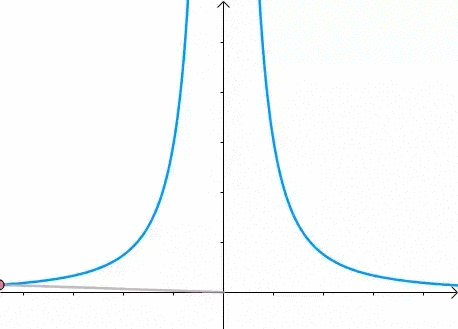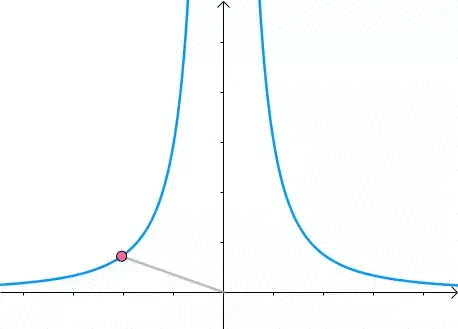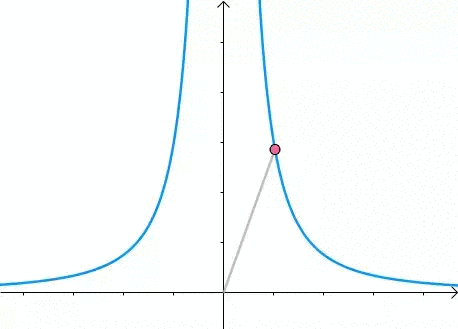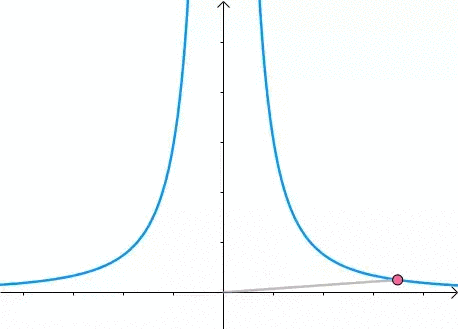
这里介绍一种解题思路。首先，与原点距离为 a 的点全部在半径为 a 的圆上：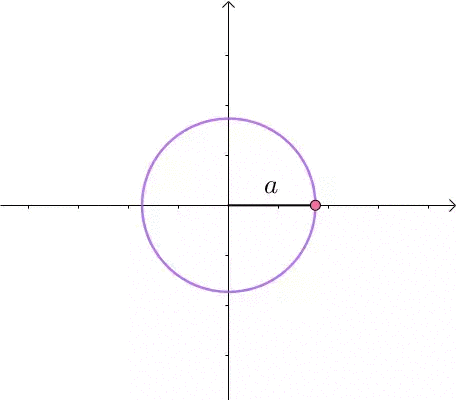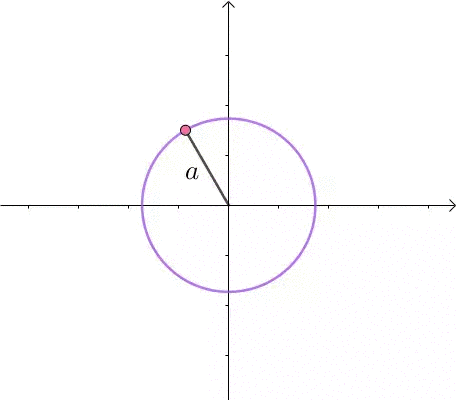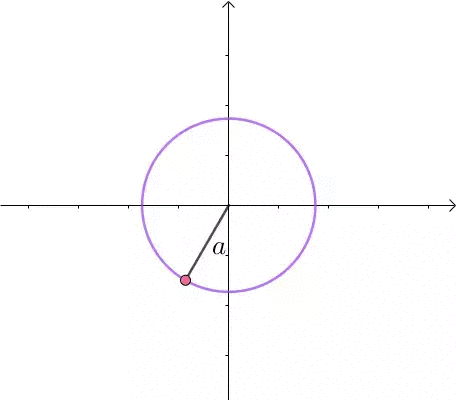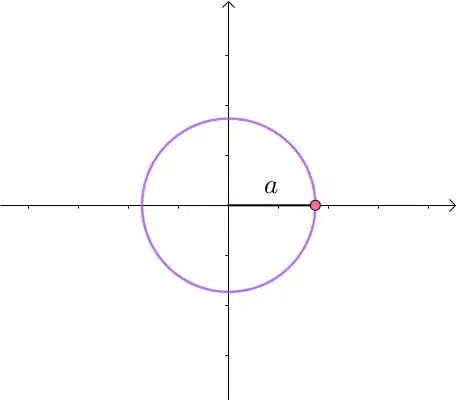
那么，我们逐渐扩大圆的半径：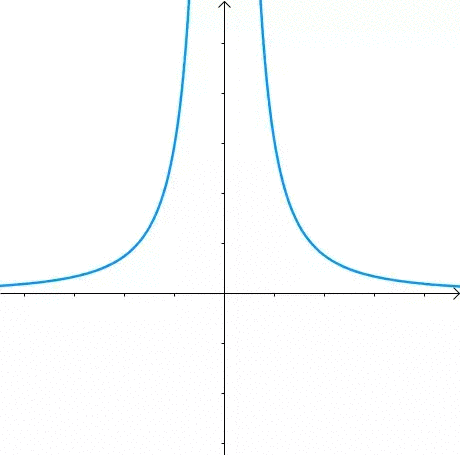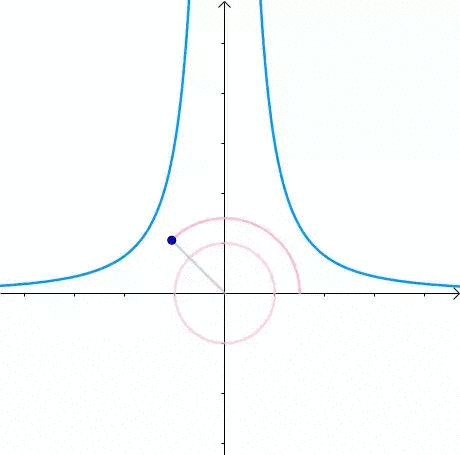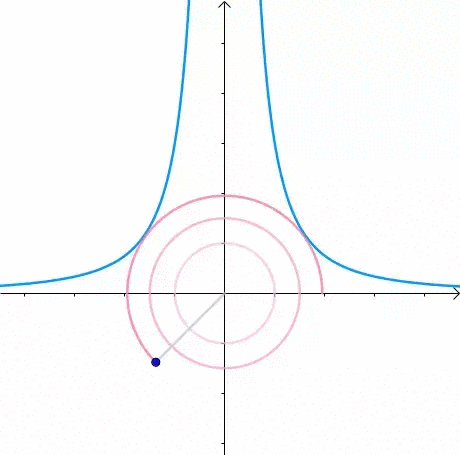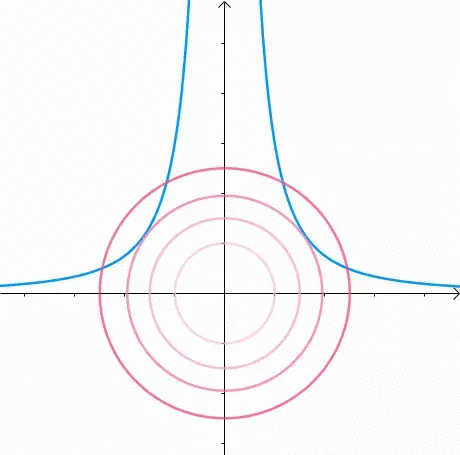
显然，第一次与 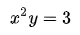相交的点就是距离原点最近的点：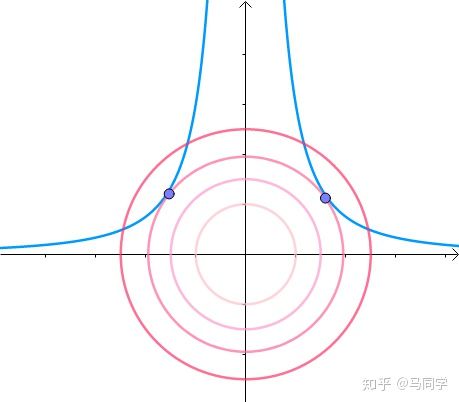
此时，圆和曲线相切，也就是在该点切线相同：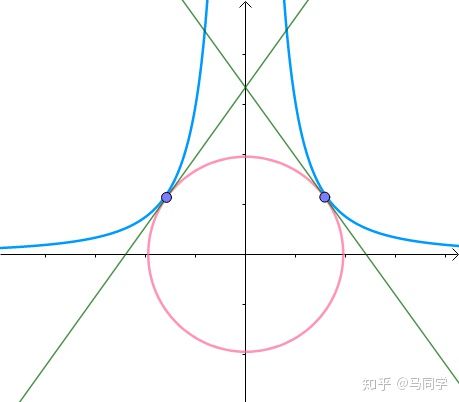
至此，我们分析出了：在极值点，圆与曲线相切
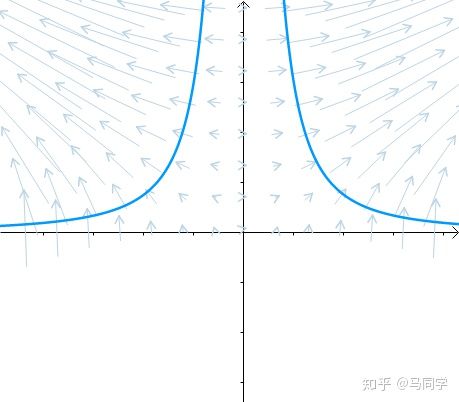
等高线
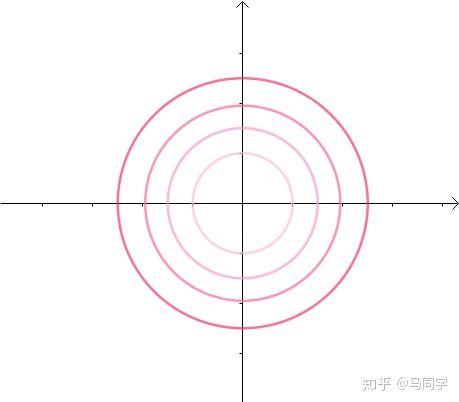
可以看作函数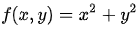 
的等高线：
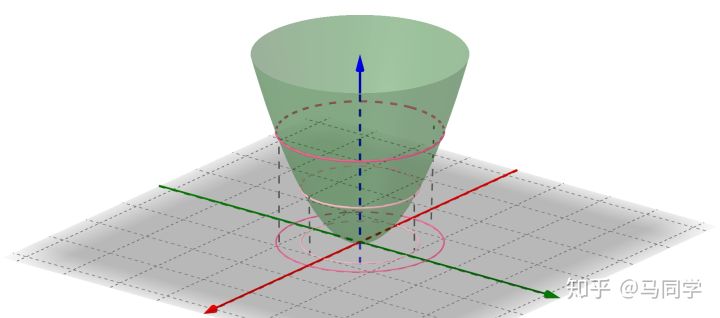
梯度向量：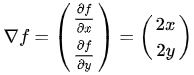
是等高线的法线：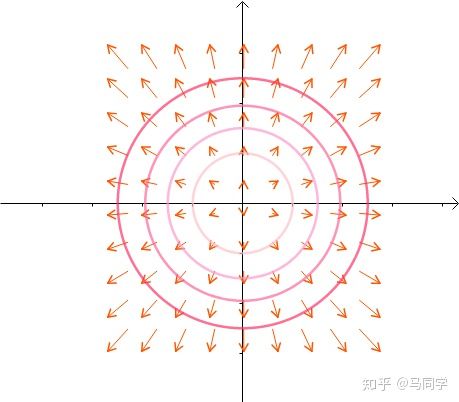
另外一个函数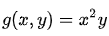 
的等高线为：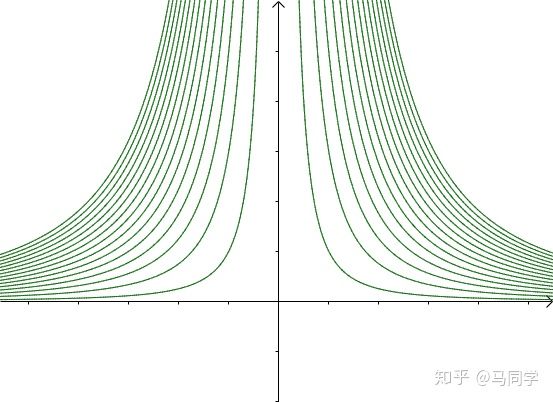
之前的曲线 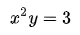就是其中值为3的等高线：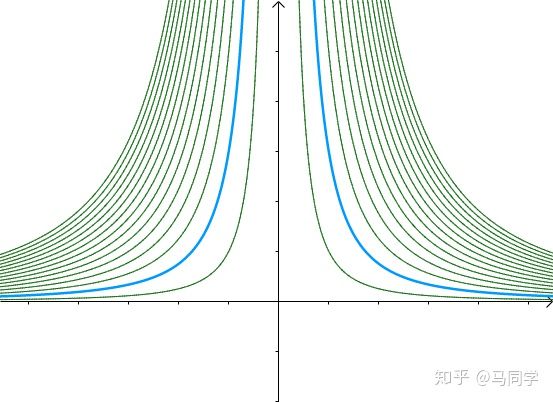
因此，梯度向量：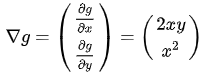
也垂直于等高线 ：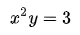
梯度向量是等高线的法线，更准确地表述是：梯度与等高线的切线垂直
拉格朗日乘子法
求解
根据之前的两个分析：
- 在极值点，圆与曲线相切
- 梯度与等高线的切线垂直
综合可知，在相切点，圆的梯度向量和曲线的梯度向量平行：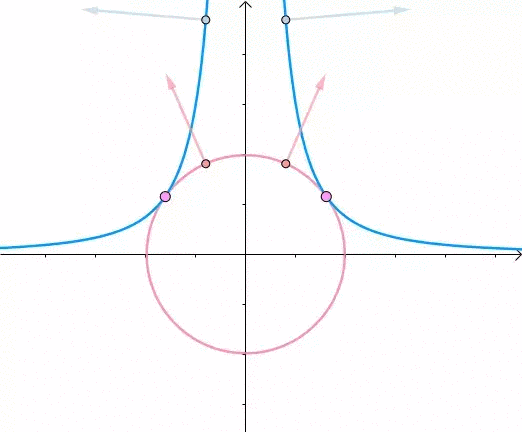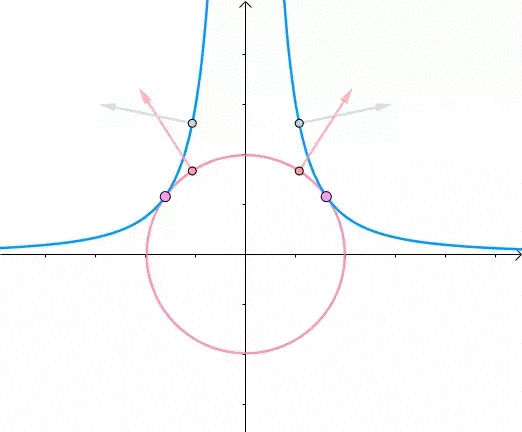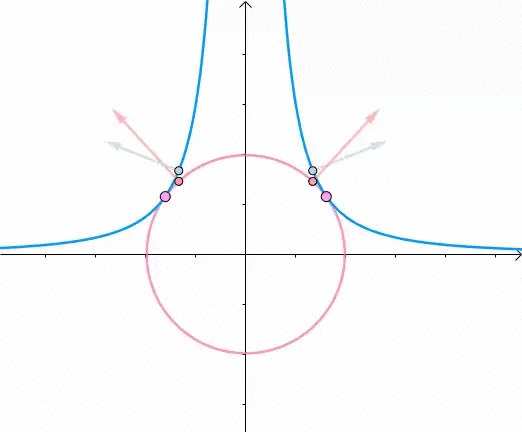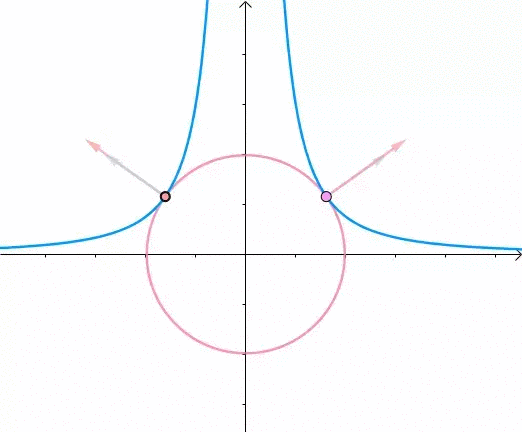
也就是梯度向量平行，用数学符号表示为：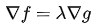
还必须引入 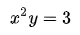这个条件，否则这么多等高线，不知道指的是哪一根：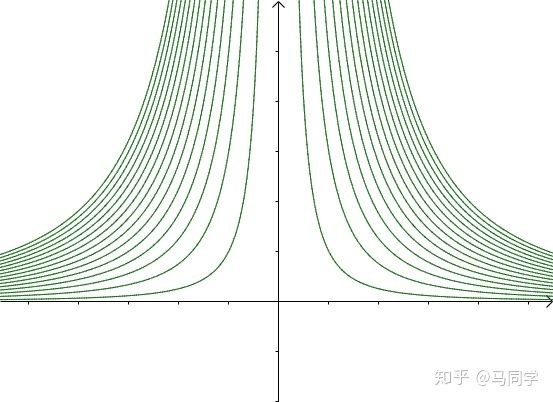
因此联立方程：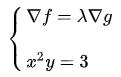
求一下试试：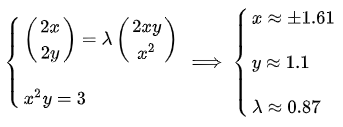
这就是拉格朗日乘子法。
定义
要求函数 f 在 g 约束下的极值这种问题可以表示为：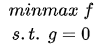
s.t. 意思是subject to，服从于，约束于的意思。
可以列出方程组进行求解：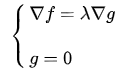
用这个定义来翻译下刚才的例子，要求：
令：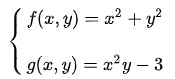
求：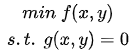
联立方程进行求解：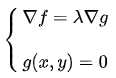
变形
这个定义还有种变形也比较常见，要求：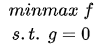
定义：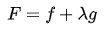
求解下面方程组即可得到答案：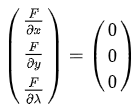
把等式左边的偏导算出来就和上面的定义是一样的了。
多个约束条件
如果增加一个约束条件呢？比如说：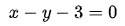
求：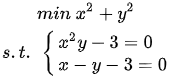
从图上看约束条件是这样的：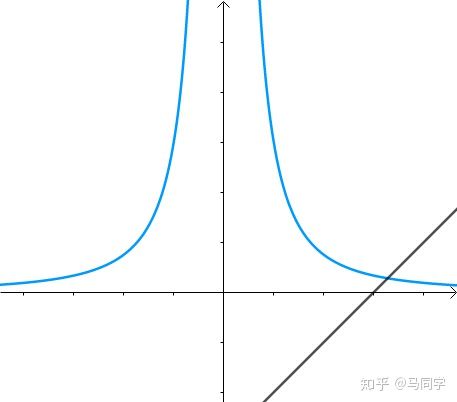
很显然所求的距离是这样的：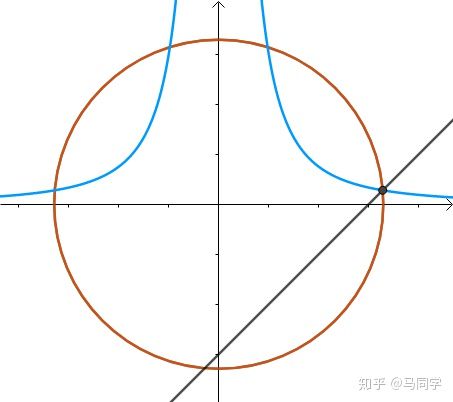
那这三者的法线又有什么关系呢？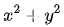
的法线是 
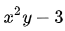和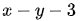 
的法线的线性组合：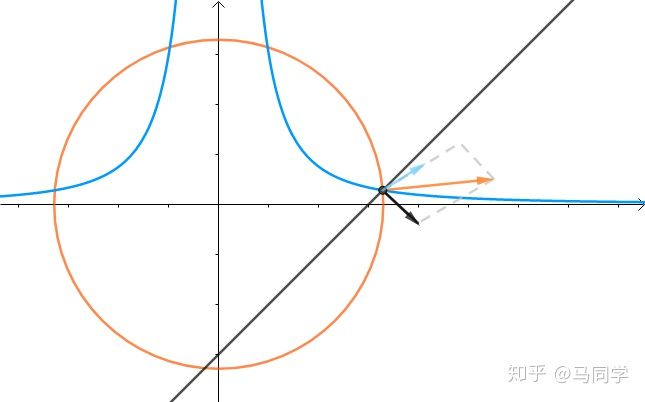
假设：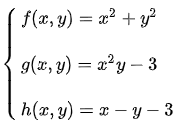
那么线性组合就表示为：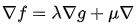
联立方程：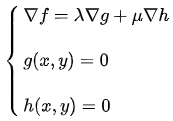
即可求解。