0%
[build by hexo/next/gitalk/hexo-generator-search/LaTeX]">
数据结构
树
- 前缀树(字典树)
- 前缀树又名字典树,单词查找树,Trie 树,是一种多路树形结构,是哈希树的变种,和hash效率有一拼,是一种用于快速检索的多叉树结构。
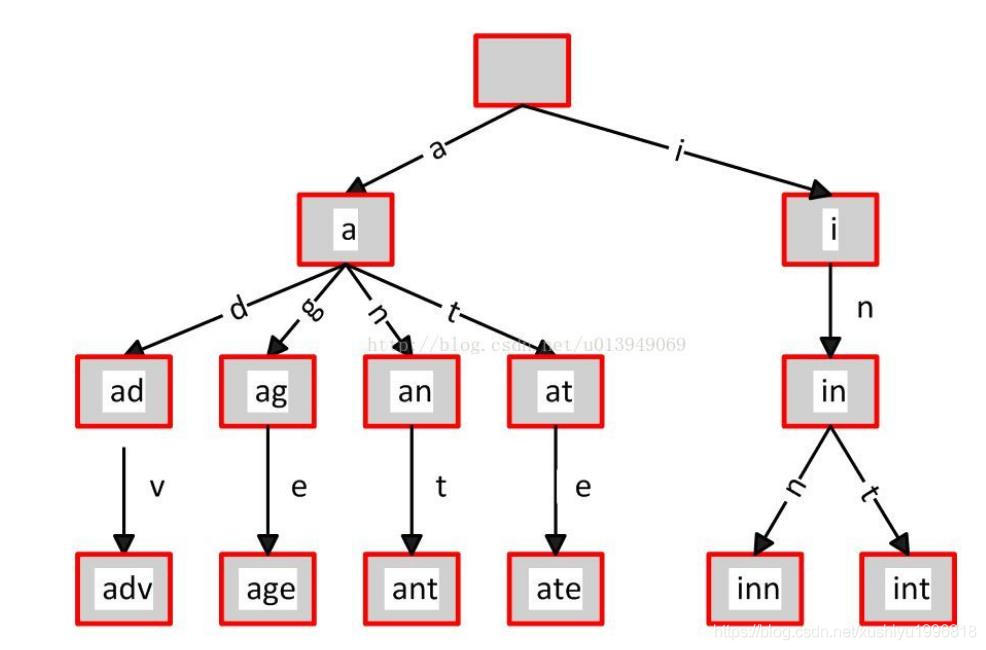
- 特性
- 根节点不包含字符,除根节点外的每一个子节点都包含一个字符。
- 从根节点到某一节点的路径上的字符连接起来,就是该节点对应的字符串。
- 每个节点的所有子节点包含的字符都不相同。
- 每条边对应一个字母。每个节点对应一项前缀。叶节点对应最长前缀,即单词本身。
- 应用场景
- 字符串的快速检索
- 字符串排序
- 最长公共前缀
- 自动匹配前缀显示后缀
- B树
- 即二叉搜索树
- 结构特点
- 所有非叶子结点至多拥有两个儿子(Left 和 Right);
- 所有结点存储一个关键字;
- 非叶子结点的左指针指向小于其关键字的子树,右指针指向大于其关键字的子树;
- B-树
- B-tree,即 B树,而不要读成 B减树,它是一种多路搜索树(并不是二叉的)
- 结构特点
- 定义任意非叶子结点最多只有 M 个儿子;且 M>2;
- 根结点的儿子数为
[2, M];
- 除根结点以外的非叶子结点的儿子数为
[M/2, M];
- 每个结点存放至少 M/2-1(取上整)和至多 M-1 个关键字;(至少2个关键字)
- 非叶子结点的关键字个数=指向儿子的指针个数-1;
- 非叶子结点的关键字:
K[1], K[2], …, K[M-1];且 K[i] < K[i+1];
- 非叶子结点的指针:
P[1], P[2], …, P[M];其中 P[1] 指向关键字小 于K[1] 的子树,P[M] 指向关键字大于 K[M-1] 的子树,其它 P[i] 指向关键字属于(K[i-1], K[i])的子树;
- 所有叶子结点位于同一层;
- 特性
- 关键字集合分布在整颗树中;
- 任何一个关键字出现且只出现在一个结点中;
- 搜索有可能在非叶子结点结束;
- 其搜索性能等价于在关键字全集内做一次二分查找;
- 自动层次控制;
- 如果索引是采用 B 树结构存储的,所以对应的索引项并不会被删除,经过一段时间的增删改操作后,数据库中就会出现大量的存储碎片,这和磁盘碎片、内存碎片产生原理是类似的,这些存储碎片不仅占用了存储空间,而且降低了数据库运行的速度。如果发现索引中存在过多的存储碎片的话就要进行 “碎片整理”了,最方便的“碎片整理” 手段就是重建索引, 重建索引会将先前创建的索引删除然后重新创建索引
- B+树
- B+树是B-树的变体,也是一种多路搜索树
- 结构特点
- 其定义基本与 B-树同,除了:
- 非叶子结点的子树指针与关键字个数相同;
- 非叶子结点的子树指针 P[i],指向关键字值属于
(K[i], K[i+1])的子树(B-树是开区间);
- 为所有叶子结点增加一个链指针;
- 所有关键字都在叶子结点出现;
- 特性
- 所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的;
- 不可能在非叶子结点命中;
- 非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层;
- 更适合文件索引系统;
- 原因
- B+树空间利用率更高,因为 B+树的内部节点只是作为索引使用,而不像 B-树那样每个节点都需要存储硬盘指针。
- 增删文件(节点)时,效率更高,因为 B+树的叶子节点包含所有关键字,并以有序的链表结构存储,这样可很好提高增删效率。
- B*树
- 是 B+树的变体,在 B+树的非根和非叶子结点再增加指向兄弟的指针
- 平衡二叉树
- AVL 树
- 平衡二叉搜索树(Self-balancing binary search tree)又被称为 AVL 树(有别于 AVL 算法)
- 具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过 1,并且左右两个子树都是一棵平衡二叉树。
- 红黑树
- 是一种平衡二叉树,但每个节点有一个存储位表示节点的颜色,可以是红或黑。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制,红黑树确保没有一条路径会比其它路径长出两倍,因此,红黑树是一种弱平衡二叉树(由于是弱平衡,可以看到,在相同的节点情况下,AVL树的高度<=红黑树),相对于要求严格的 AVL 树来说,它的旋转次数少,所以对于搜索,插入,删除操作较多的情况下,用红黑树。
- 对比
| 平衡二叉树类型 |
平衡度 |
调整频率 |
适用场景 |
| AVL树 |
高 |
高 |
查询多,增/删少 |
| 红黑树 |
低 |
低 |
增/删频繁 |
