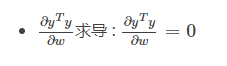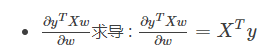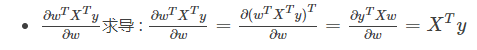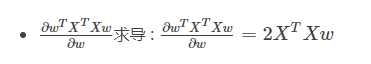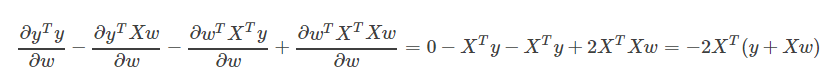转自:https://www.cnblogs.com/wlzy/p/8007045.html
前提及说明
第一次遇见矩阵求导,大多数人都是一头雾水,而搜了维基百科看也还是云里雾里,一堆的名词和一堆的表格到底都是什么呢?这里总结了我个人的学习经验,并且通过一个例子可以让你感受如何进行矩阵求导,下次再遇到需要进行矩阵求导的地方就不会措手不及。
在进行概念的解说之前,首先大家需要先知道下面的这个前提:
前提: 若 x 为向量,则默认 x 为列向量, xT 为行向量
布局的概念
布局简单地理解就是分子 y 、分母 x 是行向量还是列向量。
- 分子布局(Numerator-layout):分子为 y 或者分母为 xT (即,分子为列向量或者分母为行向量)
- 分母布局(Denominator-layout):分子为 yT 或者分母为 x (即,分子为行向量或者分母为列向量)
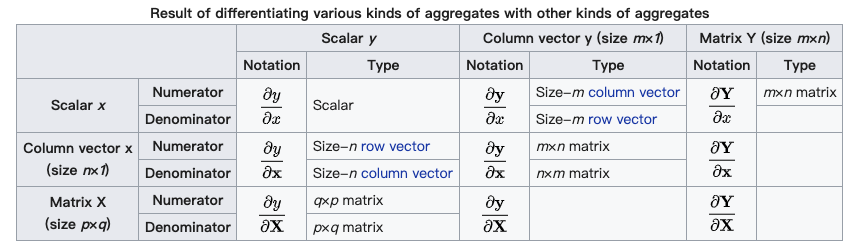
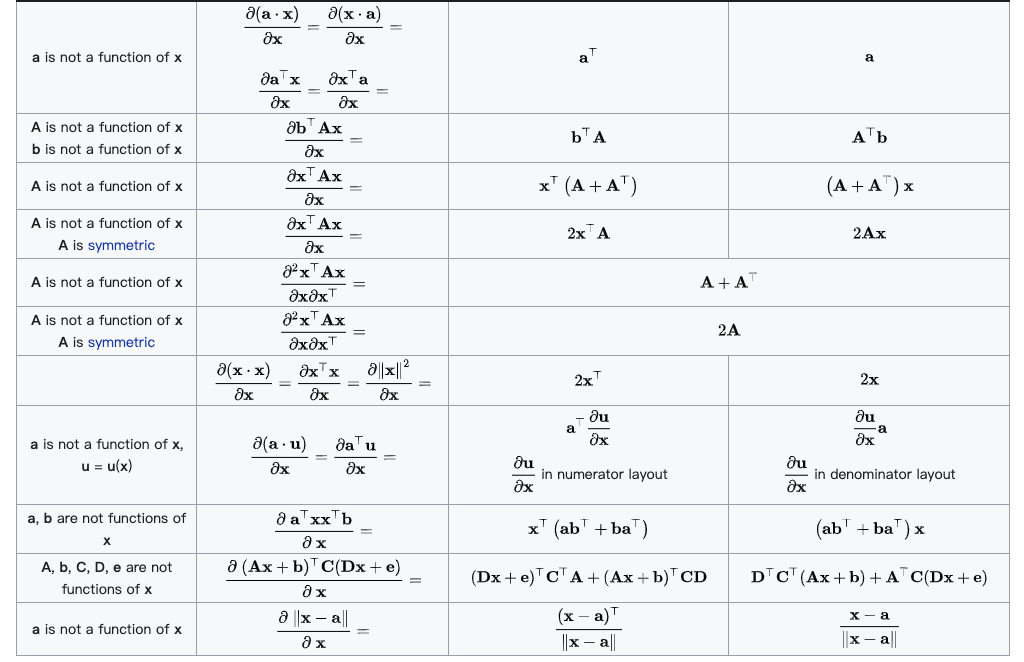
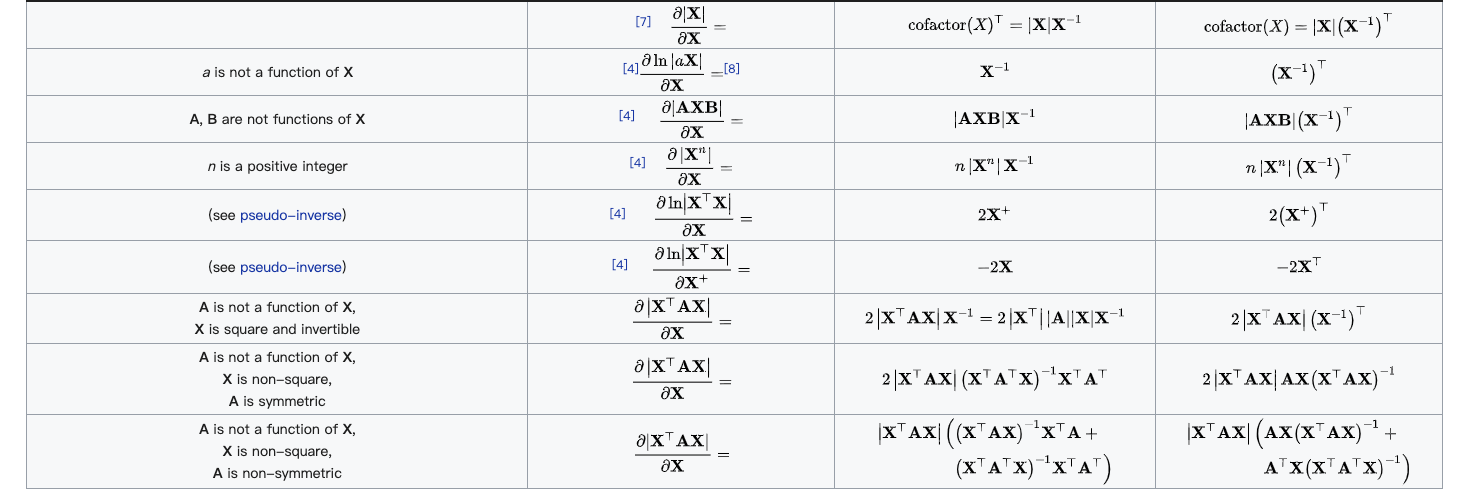
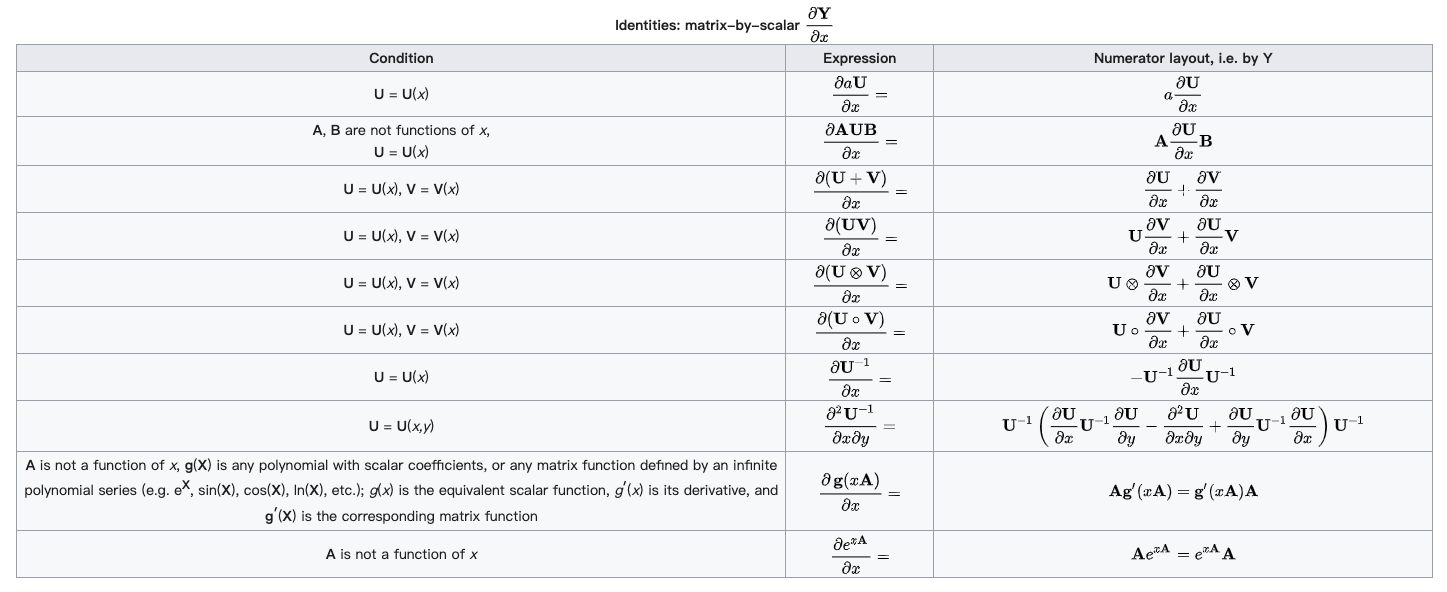
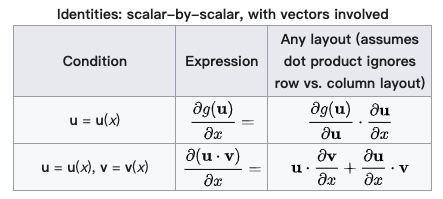
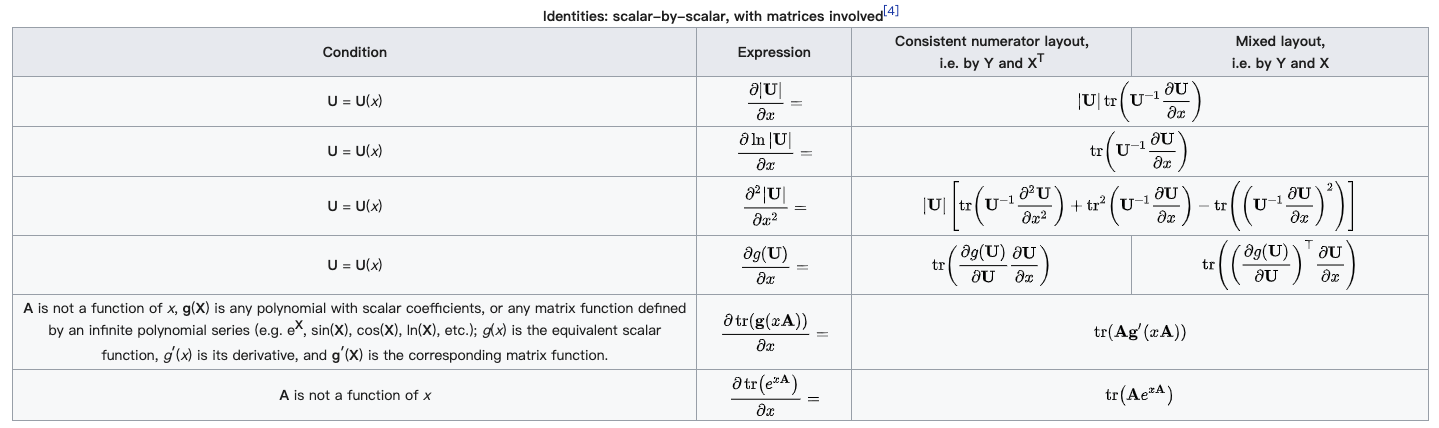
为了更加深刻地理解两种布局的特点和区别,下面是从维基百科中布局部分拿来的例子
分子布局
- 标量/向量:
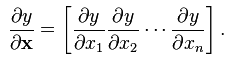 (分母的向量为行向量)
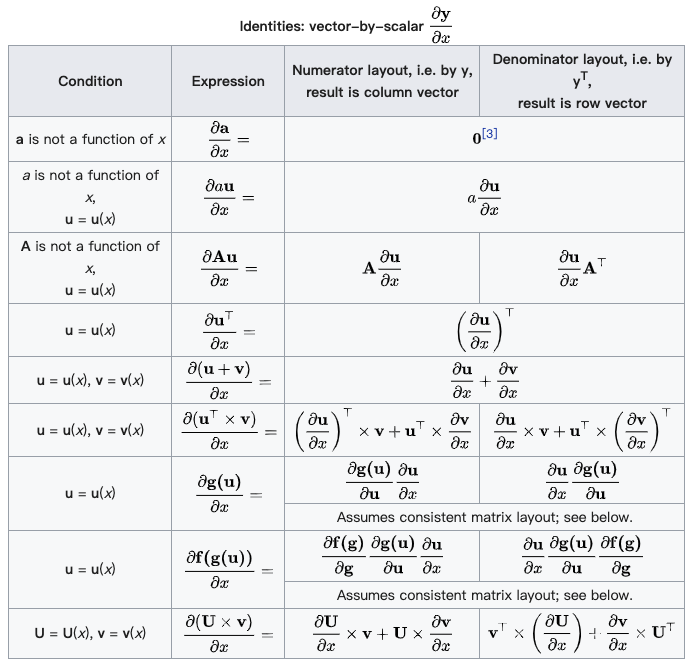
(分母的向量为行向量) - 向量/标量:
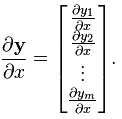 (分子的向量为列向量)
(分子的向量为列向量) - 向量/向量:
 (分子为列向量横向平铺,分母为行向量纵向平铺)
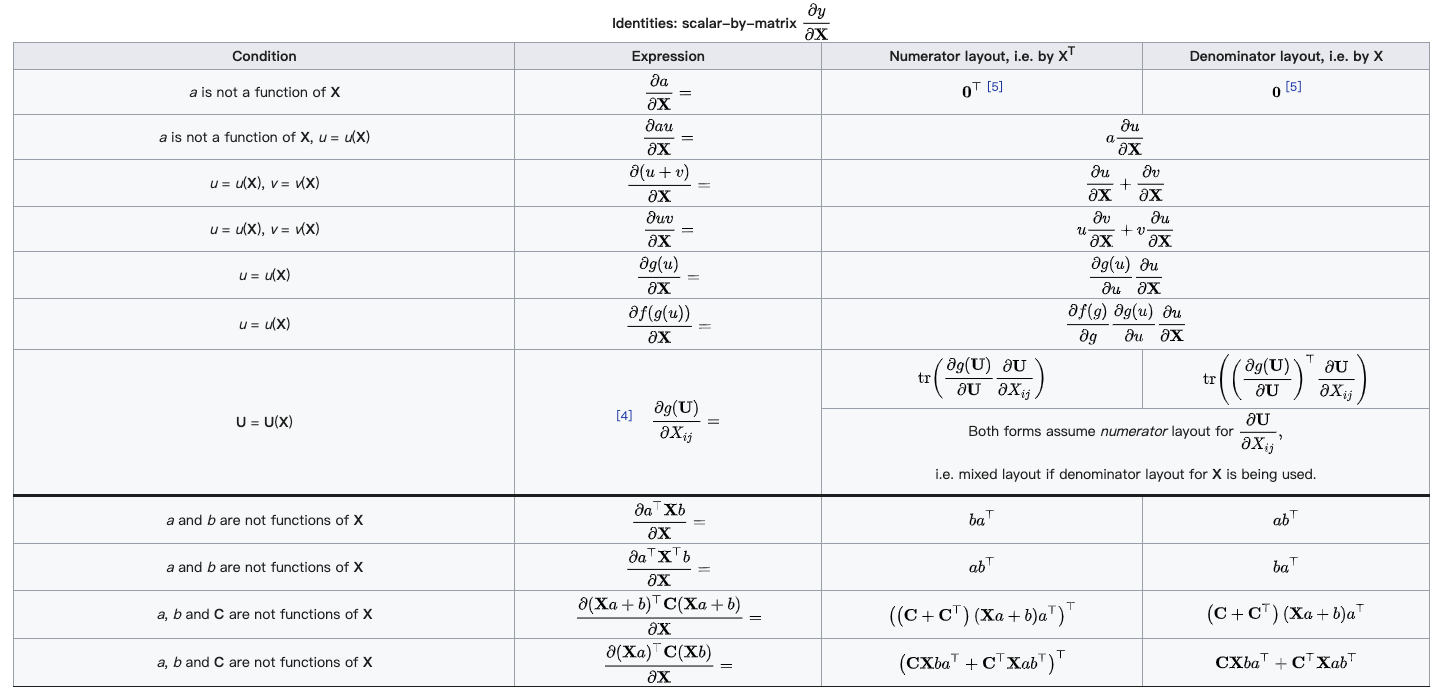
(分子为列向量横向平铺,分母为行向量纵向平铺) - 标量/矩阵:
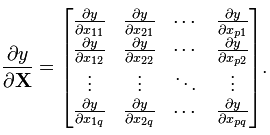 (注意这个矩阵部分是转置的,而下面的分母布局是非转置的)
(注意这个矩阵部分是转置的,而下面的分母布局是非转置的) - 矩阵/标量:
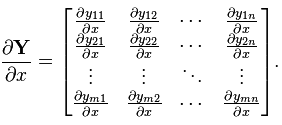
分母布局
- 标量/向量:
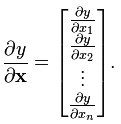 (分母的向量为列向量)
(分母的向量为列向量) - 向量/标量:
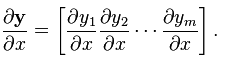 (分子的向量为行向量)
(分子的向量为行向量) - 向量/向量:
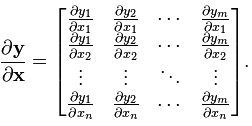 (分子为行向量纵向平铺,分母为列向量横向平铺)
(分子为行向量纵向平铺,分母为列向量横向平铺) - 标量/矩阵:
 (矩阵部分为原始矩阵)
(矩阵部分为原始矩阵)
一个求导的例子
问题
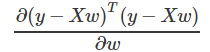
说明: y、w为列向量,X为矩阵
式子演化
看到这个例子不要急着去查表求导,先看看它的形式,是 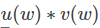 的形式,这种形式一般求导较为复杂,因此为了简化运算,我们先把式子展开成下面的样子(注意:
的形式,这种形式一般求导较为复杂,因此为了简化运算,我们先把式子展开成下面的样子(注意: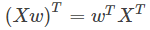 : )
: )
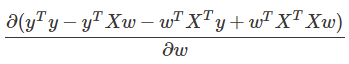
然后就可以写成四个部分求导的形式如下(累加后求导=求导后累加):
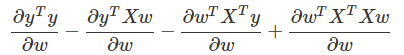
求导
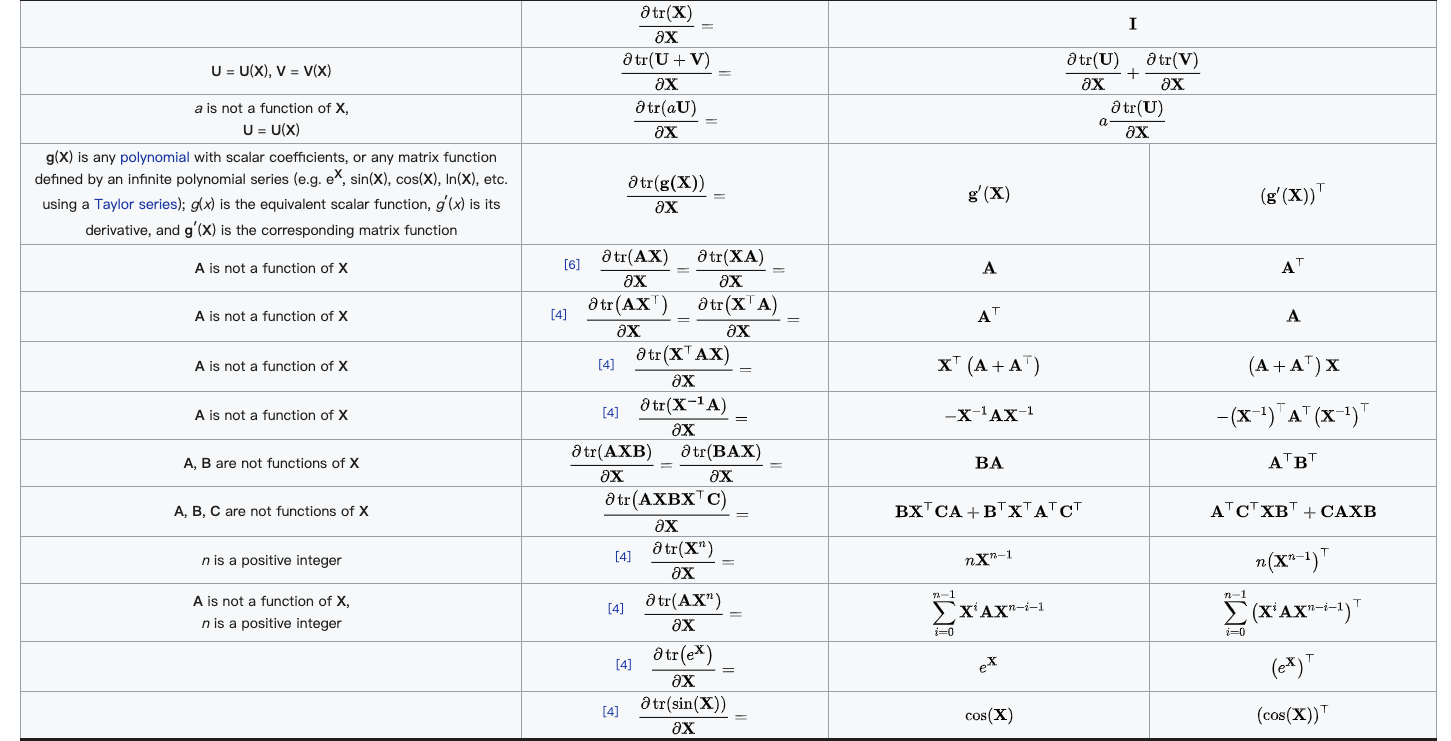
说明:分子部分为标量,分母部分为向量,找到维基百科中的Scalar-by-vector identities表格,在表格中匹配形式到第1行的位置,因为分母为列向量,因此为分母布局,对应的求导结果就是 0 。
说明:同样的,在维基百科中的Scalar-by-vector identities表格,在表格中匹配形式到第11行的位置。
说明:因为分子为标量,标量的转置等于本身,所以对分子进行转置操作,其等价于第二部分。
说明:同样的,在维基百科中的Scalar-by-vector identities表格,在表格中匹配形式到第13行的位置。
整合
把四个部分求导结果进行相应的加减就可以得到最终的结果:
分子布局,即按照 y 和xT (相比较于x)的布局。(求导结果中分子保持原始形式,分母为转置形式)
分母布局, 即按照 yT 和 x (相比较于y)。(求导结果中分子为转置形式,分母保持原始形式)
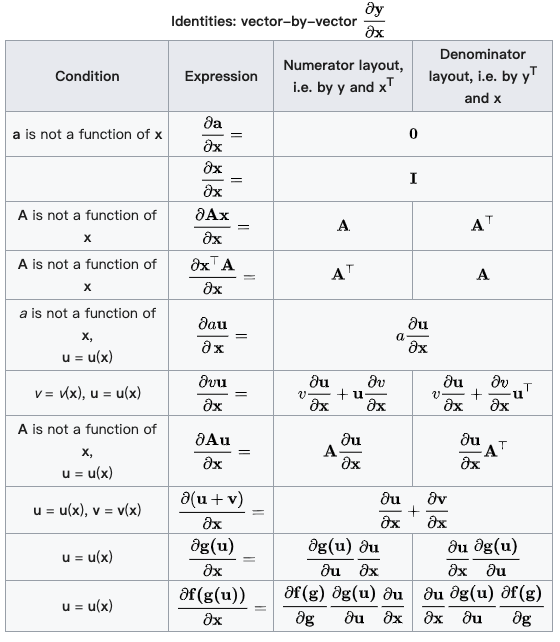
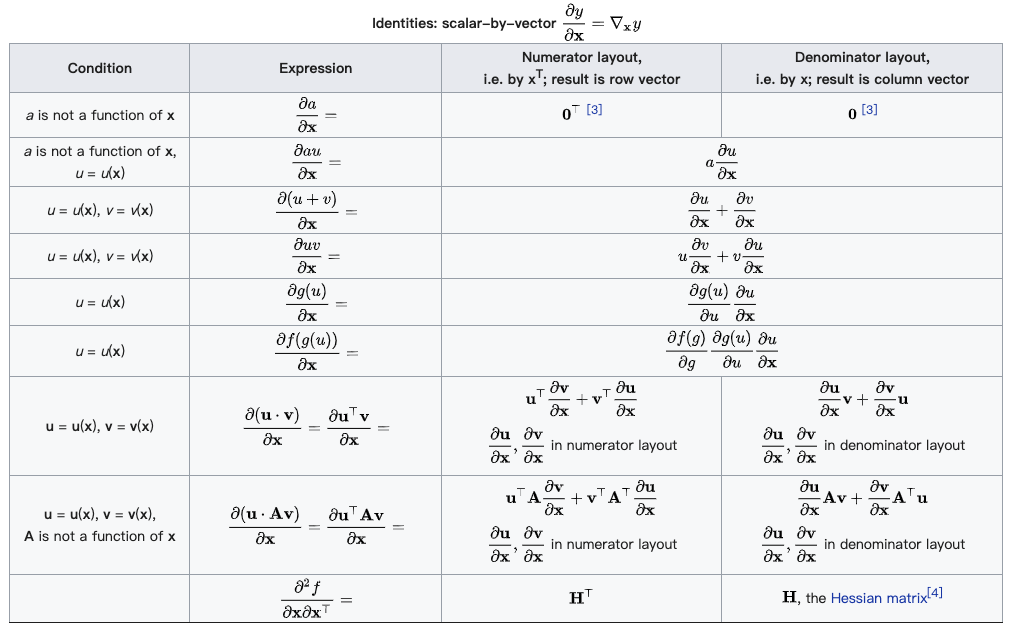
附录:公式推导
公式一
对任意行向量 $\mathbf{w} = (w_1, w_2, \cdots w_n)$ 都有
$$
\left.\frac{\partial(\mathbf{w} \mathbf{x})}{\partial \mathbf{x}}=\left[\begin{array}{c}{\frac{\partial(\mathbf{w} \mathbf{x})}{x_{1}}} \ {\frac{\partial(\mathbf{w} \mathbf{x})}{x_{2}}} \ {\vdots} \ {\frac{\partial(\mathbf{w} \mathbf{x})}{x_{n}}}\end{array}\right]=\left[\begin{array}{c}{\frac{\partial\left(w_1 x_1+w_2 x_{2}+\cdots+w_{n} x_{n}\right)}{x_{1}}} \ {\frac{\partial\left(w_{1} x_{1}+w_{2} x_{2}+\cdots+w_{n} x_{n}\right)}{x_{2}}} \ {\vdots} \ {\frac{\partial\left(w_1 x_1+w_2 x_{2}+\cdots+w_{n} x_{n}\right)}{x_{n}}}\end{array}\right]=\left[\begin{array}{c}{w_{1}} \ {w_{2}} \ {\vdots} \ {w_{n}}\end{array}\right]=\mathbf{w}^{T}\right.
$$
同时注意,如果 $\mathbf{w}$ 表示一个列向量,则
$$
\frac{\partial\left(\mathbf{x}^{\mathrm{T}} \mathbf{w}\right)}{\partial \mathbf{x}}=\mathbf{w}
$$
公式二
$\mathbf{A}$ 表示一个矩阵,其中 $\mathbf{a_1, a_2, \cdots a_n}$ 表示行向量
$$
\mathbf{A}=\left(\mathbf{a}{\mathbf{1}}, \mathbf{a}{2}, \cdots, \mathbf{a}{\mathbf{n}}\right)^{T}
$$
都有
$$
\frac{\partial(\mathbf{A} \mathbf{x})}{\partial \mathbf{x}}=\frac{\partial\left(\mathbf{a}{1} \mathbf{x}, \mathbf{a}{2} \mathbf{x}, \cdots, \mathbf{a}{\mathbf{n}} \mathbf{x}\right)^{T}}{\partial \mathbf{x}}=\left(\mathbf{a}{1}^{T}, \mathbf{a}{2}^{T}, \cdots, \mathbf{a}{\mathbf{n}}^{T}\right)=\mathbf{A}^{T}
$$
$\mathbf{B}$ 表示一个矩阵,其中 $\mathbf{b_1, b_2, \cdots b_n}$ 表示列向量
$$
\mathbf{B}=\left(\mathbf{b}{\mathbf{1}}, \mathbf{b}{2}, \cdots, \mathbf{b}{\mathbf{n}}\right)
$$
都有
$$
\frac{\partial\left(\mathbf{x}^{\mathrm{T}} \mathbf{B}\right)}{\partial \mathbf{x}}=\frac{\partial\left(\mathbf{x}^{\mathrm{T}} \mathbf{b}{1}, \mathbf{x}^{\mathrm{T}} \mathbf{b}{2}, \cdots, \mathbf{x}^{\mathrm{T}} \mathbf{b}{\mathbf{n}}\right)}{\partial \mathbf{x}}=\left(\mathbf{b}{1}, \mathbf{b}{2}, \cdots, \mathbf{b}{\mathbf{n}}\right)=\mathbf{B}
$$
公式三
$$
\frac{\partial\left(\mathbf{x}^{\mathrm{T}} \mathbf{x}\right)}{\partial \mathbf{x}}=\left[\begin{array}{c}{\frac{\partial \mathbf{x}^{\mathrm{T}} \mathbf{x}}{x_{1}}} \ {\frac{\partial \mathbf{x}^{\mathrm{T}} \mathbf{x}}{x_2}} \ {\vdots} \ {\frac{\partial \mathbf{x}^{\mathrm{T}} \mathbf{x}}{x_{n}}}\end{array}\right]=\left[\begin{array}{c}{\frac{\partial\left(x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}\right)}{x_{1}}} \ {\frac{\partial\left(x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}\right)}{x_{2}}} \ {\vdots} \ {\frac{\partial\left(x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}\right)}{x_{n}}}\end{array}\right]=\left[\begin{array}{c}{2 x_{1}} \ {2 x_{2}} \ {\vdots} \ {2 x_{n}}\end{array}\right]=2 \mathbf{x}
$$