转自:https://blog.csdn.net/qq_23947237/article/details/78265026
一个例子搞清楚(先验分布/后验分布/似然估计)
preface:
无论是《通信原理》、《信息论》、《信道编码》还是《概率与统计理论》,或者在现在流行的《模式识别》和《Machine Learning》中总会遇到这么几个概念:先验分布/后验分布/似然估计。
如果大家不熟悉这几个词,相信大家熟知贝叶斯公式,该公式涉及到了以上几个概念。但是学完本科课程,也会算题,就是在实际情境中总感觉理不清这几个概念的关系,最近上课老被老师讲的先验、后验搞得晕头转向。因此,如果您和我遇到类似的囧事,这篇文章很适合您。
声明:本文主要内容修改整理于知乎回答。
本文目标:
- 一个隔壁小哥的故事
- 故事中的因果和三个概念
- 贝叶斯公式的角色
- 最大似然估计和贝叶斯的关系
隔壁小哥的故事
隔壁小哥要去15公里外的一个公园,他可以选择步行走路,骑自行车或者开辆车,然后通过其中一种方式花了一段时间到达公园。
首先在这个事里边,大家不要关注隔壁小哥去干嘛,也许去送外卖吧:) 。言归正传,这件事中 __采用哪种交通方式是因,花了多长时间是果__。俗话说瓜熟蒂落,皆是因果;因果循环,报应不爽。要理解即将提到的概念,何为因何为果先要搞清楚。
三个概念之后验(知果求因)
隔壁小哥去公园的故事才刚刚开始,假设在这里您已经牢记住这个故事的因和果。故事仍然要接着讲,顺便带出我们的概念。
假设我们 __已经知道小哥花了1个小时到了公园__,那么你猜他是怎么去的(走路or坐车or自行车),事实上我们 __不能百分百确定他的交通方式__,我们正常人的思路是他 很大可能 是骑车过去的,当然也不排除开车过去却由于堵车严重花了很长时间,当然还有可能他是个赛跑的运动员自己一路飞跑过去的。
假设 __已经知道小哥花了3个小时才到公园__,这个时候我们猜的时候会觉得他 很大可能 是静静地走路过去的。但是假设已经 __知道小哥只花了20分钟才到公园__,那么正常人会觉得他 最大可能 是开车奔驰而去。
这种预先 __已知结果__(路上花的时间),然后根据结果 __估计(猜)原因__(交通方式)的概率分布即 __后验概率__。
例子问题公式化:P(交通方式∣花费的时间)
修改成一般的公式:P(因∣果)
公式正规化:P(θ∣x)
(公式中的 “∣|∣”读作 _given_,即给定的意思。如 P(A∣B) 即 A given B 的概率)
[解释]:看到这里估计大家很奇怪为什么要用 x、 θ 这样的字母表示,而不是熟悉的 x、 y。这样表示自然是有原因的。在这里大家只需要先暂时记住 θ 代表因、 x 代表果,后面的贝叶斯我们将会具体介绍这些字母的含义。
三个概念之先验概率(由历史求因)
换个情景,我们 不再考虑 隔壁小哥去公园的 结果 了。假设隔壁小哥还没去,大早上刚起床,打算吃完早饭再去。
假设我们比较了解小哥的个人习惯,别管怎么了解的:) 。小哥是个健身爱好者就喜欢跑步运动,这个时候我们可以猜测他更可能倾向于走路过去。
当然我的隔壁小哥是个大死肥宅,懒得要命!这个时候我们猜测他更可能倾向于坐车,连骑自行车的可能性都不大。
这个情景中隔壁小哥的交通工具选择与花费时间不再相关。因为我们是 在结果发生前 就开始猜的,根据历史规律确定 原因 (交通方式)的概率分布即 __先验概率__。
例子问题公式化:P(交通方式)
一般化:P(因)
正规化:P(θ)
三个概念之似然估计(由因求果)
换个情景,我们先重新考虑隔壁小哥去公园的交通方式。
假设隔壁小哥步行走路去,15公里的路到公园,一般情况下小哥大概要用2个多小时,当然很小的可能性是小哥是飞毛腿,跑步过去用了1个小时左右,极为小的可能是小哥是隐藏的高手,10分钟就轻功跑酷到了。
小哥决定开车,到公园半个小时是非常可能的,非常小的概率是小哥因为途径的路上有车祸堵了3个小时。
这种 __先定下来原因__,根据原因来 估计结果 的概率分布即 __似然估计__。根据原因来统计各种可能结果的概率即似然函数。
似然函数问题公式化:P(时间∣交通方式)
一般化:P(果∣因)
正规化:P(x∣θ)
贝叶斯公式
我们熟知的贝叶斯公式是这样的: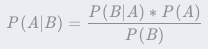
但在这里我们采用如下形式: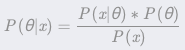

[注]:P(x) 即 evidence。隔壁小哥去公园很多次,忽略交通方式是什么,只统计每次到达公园的时间 x,于是得到了一组时间的概率分布。这种不考虑原因,只看结果的概率分布即 evidence,它也称为样本发生的概率分布的证据。
evidence 在故事中如下表示:P(时间) 或 P(果)
深入贝叶斯推断
在这里相信大多数人已经很好地理解了先验概率,后验概率,证据以及和似然估计的概念了。接下来我们将接着讲故事,隔壁小哥到公园以后去做一个游戏,游戏内容如下:
在小哥面前有两个一模一样的宝箱,一号箱子里面有3颗水果糖和1颗巧克力糖;二号箱子里面有2颗水果糖和2颗巧克力糖。
- 现在小哥将随机选择一个箱子,从中摸出一颗糖。请问小哥选择一号箱子的概率有多大?
- 现在小哥将随机选择一个箱子,从中摸出一颗糖发现是水果糖。请问这颗水果糖来自一号箱子的概率有多大?

暂且不去算这道题,在这个看似无聊的事情中,从哪个箱子去抓是 因;抓到的糖是什么糖为 结果。再去回顾我们之前的贝叶斯公式: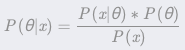
[解释]:其中 x 是观测得到的结果数据。P(x) 是观测结果数据的概率分布。如下表:
| x | 水果糖 | 巧克力糖 |
|---|---|---|
| P(x) | 5/8 | 3/8 |
[解释]:其中 θ 是决定观测结果数据分布的参数。P(θ) 是先验概率,没有观测数据的支持下 θ 发生的概率。如下表:
| θ | 一号箱 | 二号箱 |
|---|---|---|
| P(θ) | 1/2 | 1/2 |
[解释]:P(θ∣x) 是后验概率,有观测数据的支持下 θ 发生的概率。在上面的故事中第二问是小哥随机选择一个箱子,从中摸出一颗糖发现是水果糖。这颗水果糖来自一号箱子的概率就是后验概率:P(θ=一号箱∣x=水果糖)
[解释]:P(x∣θ) 是似然函数,给定某参数 θ 时结果数据的概率分布。
其中,P(θ=一号箱) 就是先验概率,根据贝叶斯公式,需求证据 P(x=水果糖) 和似然函数 _P(x=水果糖∣θ=一号箱)_。
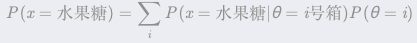
我们再考虑上面的计算:
(1) 现在小哥将随机选择一个箱子,从中摸出一颗糖。请问小哥选择一号箱子的概率。根据明显的先验知识我们就可以知道
(2) 现在小哥将随机选择一个箱子,从中摸出一颗糖发现是水果糖。请问这颗水果糖来自一号箱子的概率。后验概率为
我们为什么要在这里连续计算两道题呢,并不是为了单纯的计算,而是去比较计算结果得到贝叶斯推断的意义。
大家可以看到:没有做实验之前我们推断 P(θ=一号箱)=1/2 这个先验概率;而有了参考结果数据“从中摸出一颗糖发现是水果糖“,我们便可以得到 P(θ=一号箱∣x=水果糖)=3/5 这个后验概率。也就是说推断是一号箱的概率,在取出水果糖前和后,【θ=一号箱】事件的可能性得到了增强(1/2<3/5)。
我们可以用小哥在公园的第二个奇遇来解释【贝叶斯估计】的意义:
小哥在公园里玩飞镖,附近有个陌生人说他是一个专业的飞镖玩家,假设你现在是小哥,你可能最开始会假设这家伙在开玩笑忽悠我吧。
首先你对这个人几乎什么都不了解,但遇到一个真正的专业飞镖玩家的概率是很小的。 因为澳大利亚的专业飞镖玩家也不过大约15个。
如果这个陌生人为了证明自己,开始扔飞镖并且第一次正中靶心,但这个数据可能还是不能令你非常信服,因为你觉得这可能只是运气。
但如果这个人连续十次都正中靶心,多个观测样本让你会倾向于接受他的专业说法。
在这件事当中,你对【陌生人是专业玩家】的先验置信度就被累积的实验数据所覆盖而增强变大,贝叶斯定理起作用了。
MAP/ML/贝叶斯估计
给定一些数据样本 x,假定我们知道样本是从某一种分布中随机取出的,但我们不知道这个分布具体的参数 θ。
最大似然估计(ML,Maximum Likelihood)可以估计模型的参数。其目标是找出一组参数 θ,使得模型产生出观测数据 x 的概率最大: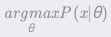
假如这个参数有一个先验概率,那么参数该怎么估计呢?这就是MAP要考虑的问题。 最大后验估计(MAP-Maxaposterior)。MAP优化的是一个后验概率,即给定了观测值后使概率最大:
前两种都是假设参数是个确定值,但贝叶斯估计假设参数是个随机数。
贝叶斯估计,假定把待估计的参数看成是符合某种先验概率分布的随机变量,而不是确定数值。在样本分布上,计算参数所有可能的情况,并通过计算参数的期望,得到后验概率密度。