转自：https://zhuanlan.zhihu.com/p/37609917
协方差矩阵在统计学和机器学习中随处可见，一般而言，可视作方差和协方差两部分组成，即方差构成了对角线上的元素，协方差构成了非对角线上的元素。本文旨在从几何角度介绍我们所熟知的协方差矩阵。
方差和协方差的定义
在统计学中，方差是用来度量单个随机变量的离散程度，而协方差则一般用来刻画两个随机变量的相似程度，其中，方差 的计算公式为
$$
\sigma_{x}^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\overline{x}\right)^{2}
$$
其中，$n$ 表示样本量，符号 $\overline{x}$ 表示观测样本的均值，这个定义在初中阶段就已经开始接触了。
在此基础上，协方差 的计算公式被定义为
$$
\sigma(x, y)=\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\overline{x}\right)\left(y_{i}-\overline{y}\right)
$$
在公式中，符号 $\overline{x}, \overline{y}$ 分别表示两个随机变量所对应的观测样本均值，据此，我们发现：方差 $\sigma^2$ 可视作随机变量 $x$ 关于其自身的协方差 $\sigma(x, x)$ .
从方差/协方差到协方差矩阵
根据方差的定义，给定 $d$ 个随机变量 $x_k, k=1, 2,…,d$ ，则这些随机变量的方差为
$$
\sigma\left(x_{k}, x_{k}\right)=\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{k i}-\overline{x}{k}\right)^{2}, k=1,2, \ldots, d
$$
其中，为方便书写，$x{ki}$ 表示随机变量 $x_k$ 中的第 $i$ 个观测样本，$n$ 表示样本量，每个随机变量所对应的观测样本数量均为 $n$。
对于这些随机变量，我们还可以根据协方差的定义，求出 两两之间的协方差__，即
$$
\sigma\left(x{m}, x{k}\right)=\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{m i}-\overline{x}{m}\right)\left(x{k i}-\overline{x}{k}\right)
$$
因此，__协方差矩阵_ 为
$$
\Sigma=\left[\begin{array}{ccc}{\sigma\left(x_{1}, x_{1}\right)} & {\cdots} & {\sigma\left(x_{1}, x_{d}\right)} \ {\vdots} & {\ddots} & {\vdots} \ {\sigma\left(x_{d}, x_{1}\right)} & {\cdots} & {\sigma\left(x_{d}, x_{d}\right)}\end{array}\right] \in \mathbb{R}^{d \times d}
$$
其中，对角线上的元素为各个随机变量的方差，非对角线上的元素为两两随机变量之间的协方差，根据协方差的定义，我们可以认定：矩阵 $\Sigma$ 为对称矩阵(symmetric matrix)，其大小为 $d \times d$ 。
多元正态分布与线性变换
假设一个向量 $x$ 服从均值向量为 $\mu$ 、协方差矩阵为 $\Sigma$ 的多元正态分布(multi-variate Gaussian distribution)，则
$$
p(\boldsymbol{x})=|2 \pi \Sigma|^{-1 / 2} \exp \left(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{T} \Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right)
$$
令该分布的均值向量为 $\mu = 0$，由于指数项外面的系数 $|2 \pi \Sigma|^{-1 / 2}$ 通常作为常数，故可将多元正态分布简化为
$$
p(\boldsymbol{x}) \propto \exp \left(-\frac{1}{2} \boldsymbol{x}^{T} \Sigma^{-1} \boldsymbol{x}\right)
$$
再令 $\boldsymbol{x}=(y, z)^{T}$，包含两个随机变量 $y$ 和 $z$，则协方差矩阵可写成如下形式：
$$
\Sigma=\left[\begin{array}{ll}{\sigma(y, y)} & {\sigma(y, z)} \ {\sigma(z, y)} & {\sigma(z, z)}\end{array}\right] \in \mathbb{R}^{2 \times 2}
$$
用单位矩阵(identity matrix) $I$ 作为协方差矩阵，随机变量 $y$ 和 $x$ 的方差均为1，则生成如干个随机数如图1所示。
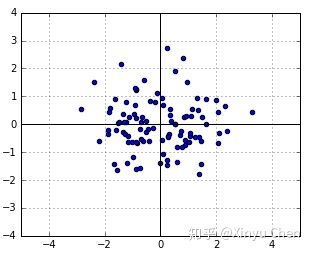（图1 标准的二元正态分布）
在生成的若干个随机数中，每个点的似然为
$$
\mathcal{L}(\boldsymbol{x}) \propto \exp \left(-\frac{1}{2} \boldsymbol{x}^{T} \boldsymbol{x}\right)
$$
对图1中的所有点考虑一个线性变换(linear transformation)： $t = Ax$，我们能够得到图2.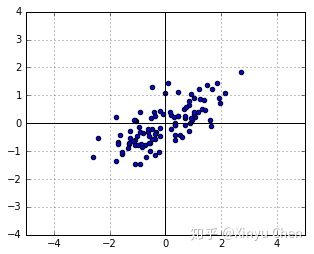
（图1 标准的二元正态分布）
图2 经过线性变换的二元正态分布，先将图1的纵坐标压缩0.5倍，再将所有点逆时针旋转30°得到。
在线性变换中，矩阵 $A$ 被称为变换矩阵(transformation matrix)，为了将图1中的点经过线性变换得到我们想要的图2，其实我们需要构造两个矩阵：
- 尺度矩阵(scaling matrix)：
$$
S=\left[\begin{array}{ll}{s_{y}} & {0} \ {0} & {s_{z}}\end{array}\right]
$$ - 旋转矩阵(rotation matrix)
$$
R=\left[\begin{array}{cc}{\cos (\theta)} & {-\sin (\theta)} \ {\sin (\theta)} & {\cos (\theta)}\end{array}\right]
$$
其中，$\theta$ 为顺时针旋转的度数。
变换矩阵、尺度矩阵和旋转矩阵三者的关系式：$A = RS$
在这个例子中，尺度矩阵为 $S=\left[\begin{array}{cc}{1} & {0} \ {0} & {\frac{1}{2}}\end{array}\right]$ ，旋转矩阵为 $R=\left[\begin{array}{cc}{\cos \left(-\frac{\pi}{6}\right)} & {-\sin \left(-\frac{\pi}{6}\right)} \ {\sin \left(-\frac{\pi}{6}\right)} & {\cos \left(-\frac{\pi}{6}\right)}\end{array}\right]=\left[\begin{array}{cc}{\frac{\sqrt{3}}{2}} & {\frac{1}{2}} \ {-\frac{1}{2}} & {\frac{\sqrt{3}}{2}}\end{array}\right]$ ，故变换矩阵为 $A=R S=\left[\begin{array}{cc}{\frac{\sqrt{3}}{2}} & {\frac{1}{4}} \ {-\frac{1}{2}} & {\frac{\sqrt{3}}{4}}\end{array}\right]$
另外，需要考虑的是，经过了线性变换，$t$ 的分布是什么样子呢？
将 $x = A^{-1}t$ 带入前面给出的似然 $\mathcal{L}(\boldsymbol{t})$ ，有
$$
\begin{array}{l}{\mathcal{L}(\boldsymbol{t}) \propto \exp \left(-\frac{1}{2}\left(A^{-1} \boldsymbol{t}\right)^{T}\left(A^{-1} \boldsymbol{t}\right)\right)} \ {=\exp \left(-\frac{1}{2} \boldsymbol{t}^{T}\left(\boldsymbol{A} \boldsymbol{A}^{T}\right)^{-1} \boldsymbol{t}\right)}\end{array}
$$
由此可以得到，多元正态分布的协方差矩阵为
$$
\Sigma=A A^{T}=\left[\begin{array}{cc}{\frac{\sqrt{3}}{2}} & {\frac{1}{4}} \ {-\frac{1}{2}} & {\frac{\sqrt{3}}{4}}\end{array}\right]\left[\begin{array}{cc}{\frac{\sqrt{3}}{2}} & {-\frac{1}{2}} \ {\frac{1}{4}} & {\frac{\sqrt{3}}{4}}\end{array}\right]=\left[\begin{array}{cc}{\frac{13}{16}} & {-\frac{3 \sqrt{3}}{16}} \ {-\frac{3 \sqrt{3}}{16}} & {\frac{7}{16}}\end{array}\right]
$$
协方差矩阵的特征值分解
回到我们已经学过的线性代数内容，对于任意对称矩阵 $\Sigma$，存在一个特征值分解(eigenvalue decomposition, EVD)：$\Sigma = U\Lambda U^T$
其中，$U$ 的每一列都是相互正交的特征向量，且是单位向量，满足 $U^TU=I$，$\Lambda$ 对角线上的元素是从大到小排列的特征值，非对角线上的元素均为0。
当然，这条公式在这里也可以很容易地写成如下形式：
$$
\Sigma=\left(U \Lambda^{1 / 2}\right)\left(U \Lambda^{1 / 2}\right)^{T}=A A^{T}
$$
其中， $A = U\Lambda^{1/2}$ ，因此，通俗地说，任意一个协方差矩阵都可以视为线性变换的结果。
在上面的例子中，特征向量构成的矩阵为
$$
U=R=\left[\begin{array}{cc}{\cos (\theta)} & {-\sin (\theta)} \ {\sin (\theta)} & {\cos (\theta)}\end{array}\right]=\left[\begin{array}{cc}{\frac{\sqrt{3}}{2}} & {\frac{1}{2}} \ {-\frac{1}{2}} & {\frac{\sqrt{3}}{2}}\end{array}\right]
$$
特征值构成的矩阵为
$$
\Lambda=S S^{T}=\left[\begin{array}{cc}{s_{y}^{2}} & {0} \ {0} & {s_{z}^{2}}\end{array}\right]=\left[\begin{array}{cc}{1} & {0} \ {0} & {\frac{1}{4}}\end{array}\right]
$$
到这里，我们发现：多元正态分布的概率密度是由协方差矩阵的特征向量控制旋转(rotation)，特征值控制尺度(scale)，除了协方差矩阵，均值向量会控制概率密度的位置，在图1和图2中，均值向量为 $0$，因此，概率密度的中心位于坐标原点。