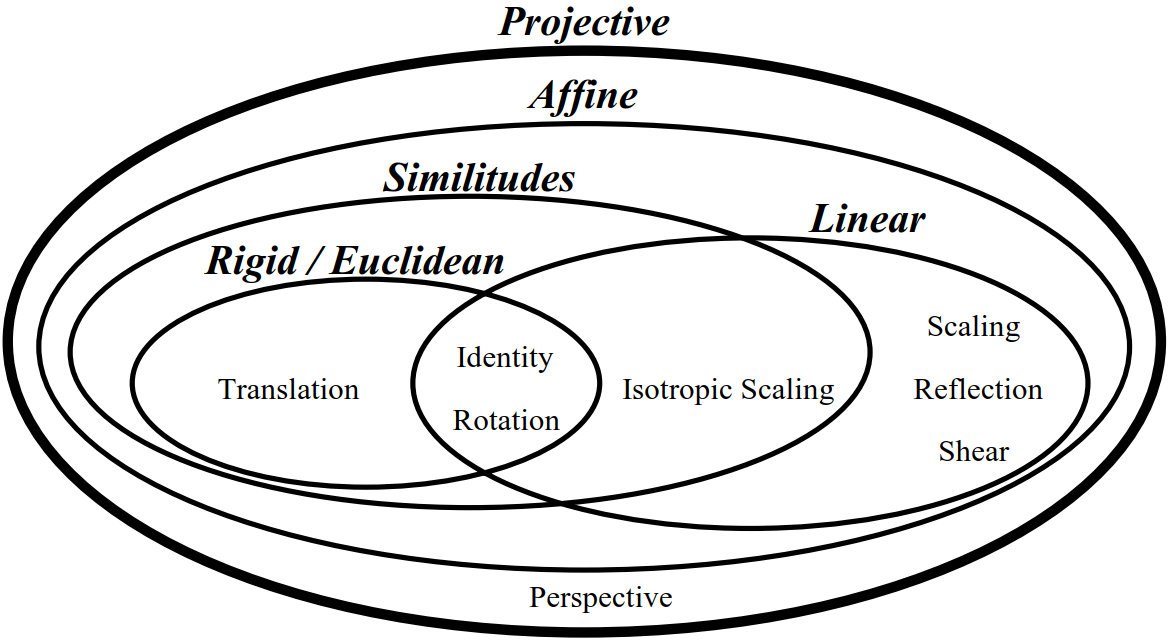
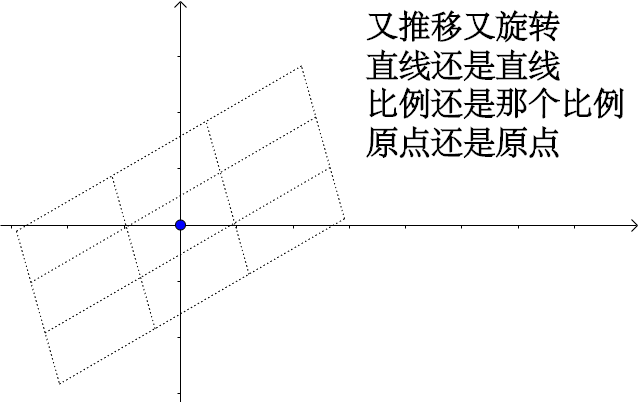
- 线性变换(linear transformation):在两个向量空间(包括由函数构成的抽象的向量空间)之间的一种保持向量加法和标量乘法的特殊映射。【就要求变换前后的加法和数乘运算不变】【旋转(rotation)、镜像(翻转)(reflection)、伸缩(缩放)(scaling),推移(错切)(shear)】
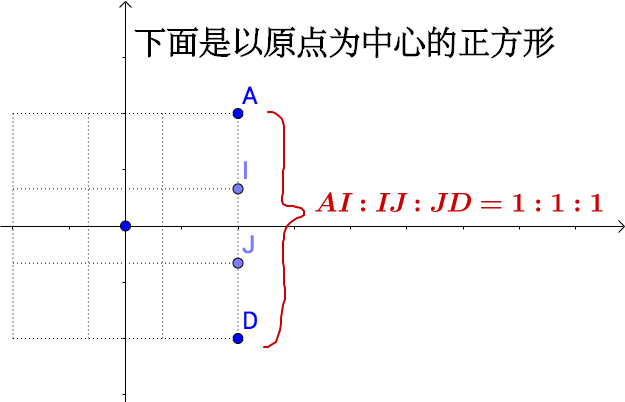
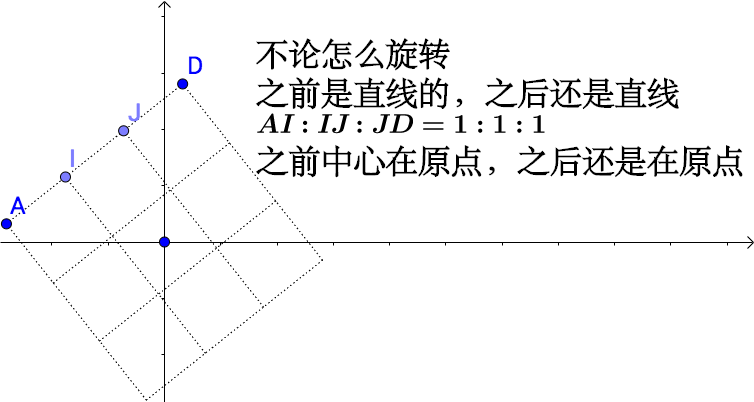
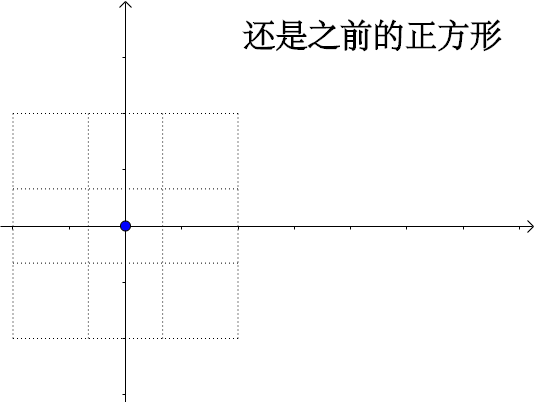
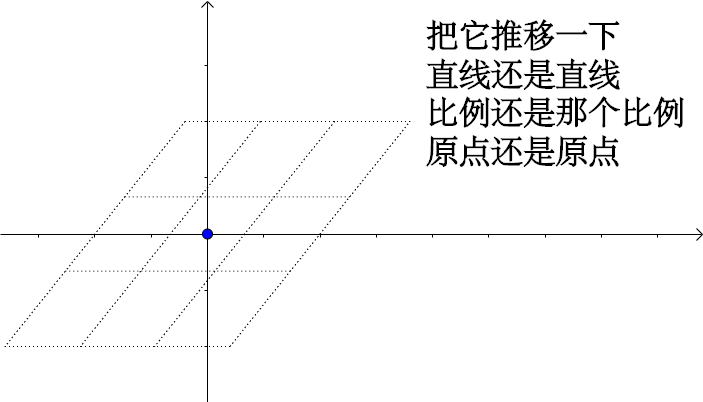
- 变换前是直线的,变换后依然是直线
- 直线比例保持不变
- 变换前是原点的,变换后依然是原点
- 刚体变换(rigid transformation)或欧式变换(Euclidean transformation):在三维空间中,当物体不发生形变时,对一个几何物体作旋转、平移的运动,称为刚体变换。【可以理解为保持长度,角度,面积等不变的仿射变换, 即保持内积和度量不变】【平移(translation)、旋转(rotation)】
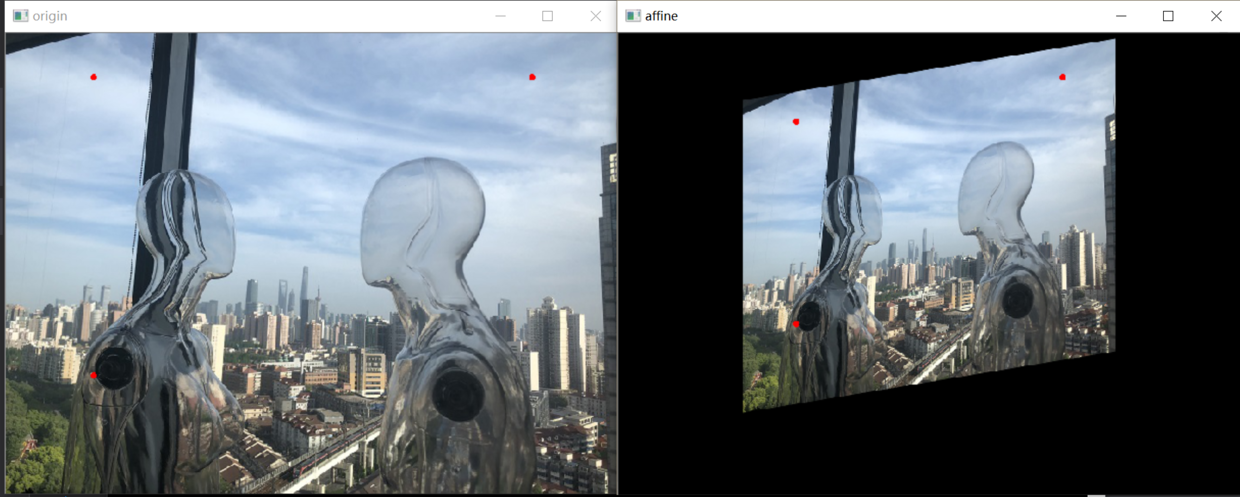
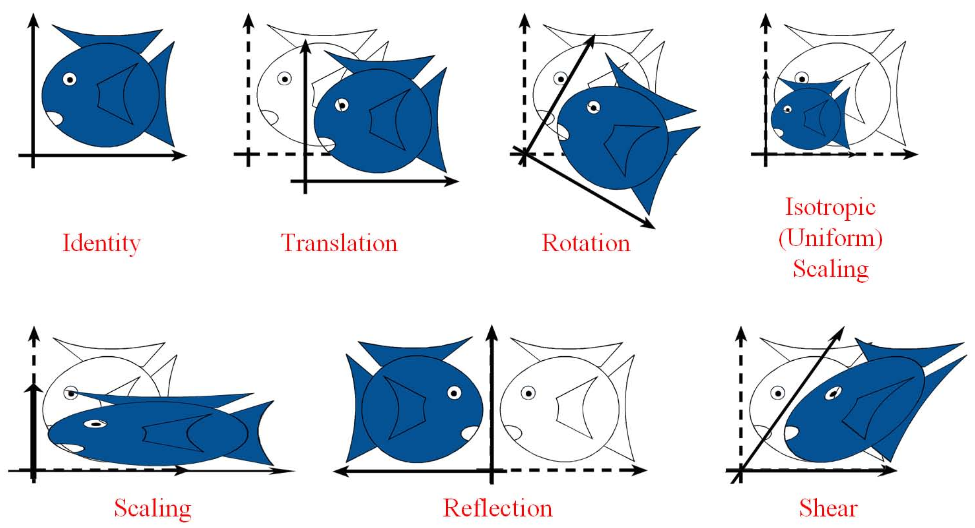
- 仿射变换:指在几何中,一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间。【线性变换 + 平移(translation)】【保证物体形状的“平直性”和“平行性”】
- 变换前是直线的,变换后依然是直线
- 直线比例保持不变
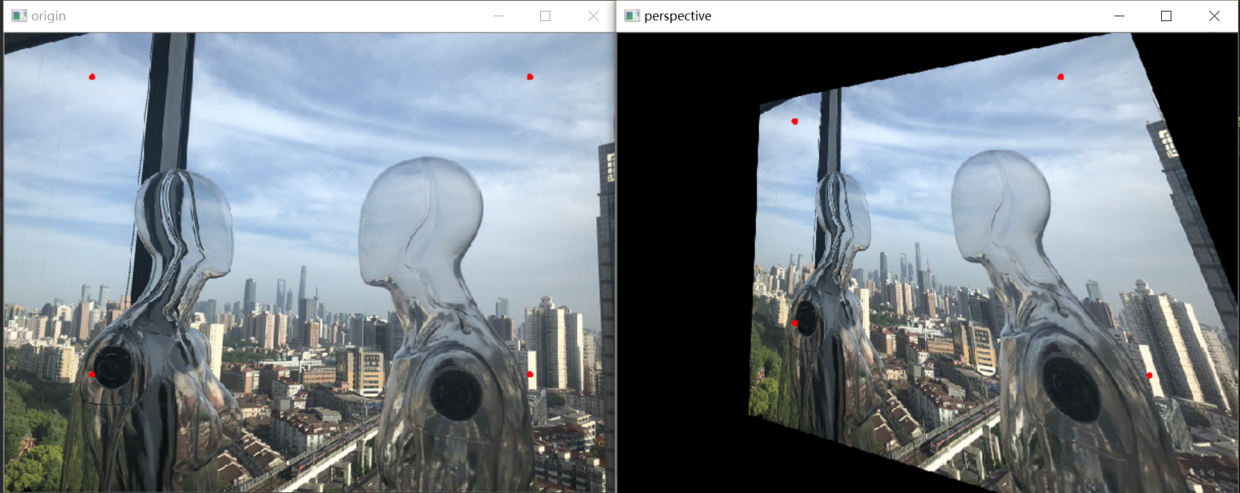
- 透视变换(perspective transformation)或投影变换(projective transformation):利用透视中心、像点、目标点三点共线的条件,按透视旋转定律使承影面(透视面)绕迹线(透视轴)旋转某一角度,破坏原有的投影光线束,仍能保持承影面上投影几何图形不变的变换。【仿射变换是透视变换的子集,仿射变换是特殊的透射变换】【不能保证物体形状的“平行性”】
- 相似变换(similarity transformation):【刚体变换 + uniform scaling】
基础概念
放缩(scaling)可进一步分为 uniform scaling 和 non-uniform scaling,前者每个坐标轴放缩系数相同(各向同性),后者不同;如果放缩系数为负,则会叠加上反射(reflection)—— reflection可以看成是特殊的 scaling。





线性变换
仿射变换
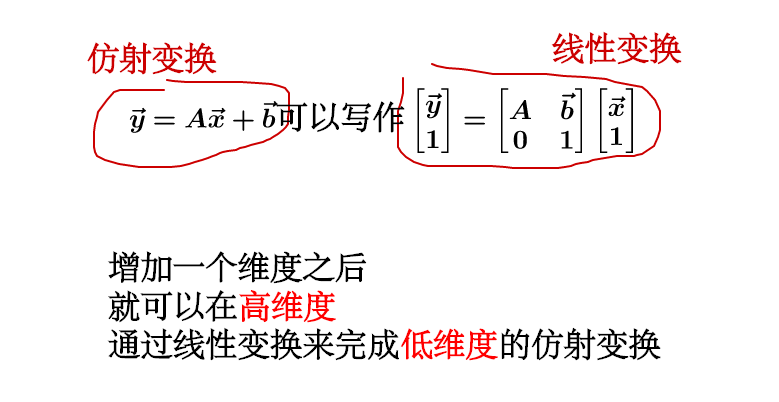
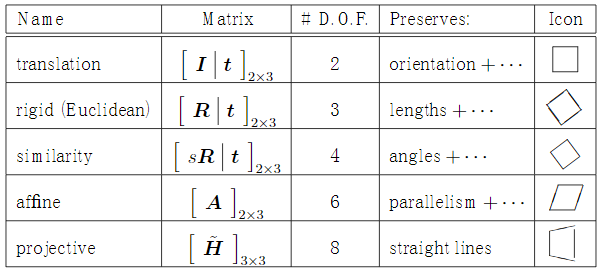
为了涵盖平移,引入齐次坐标,在原有2维坐标的基础上,增广1个维度,如下所示:
$$
\left[\begin{array}{l}{x^{\prime}} \ {y^{\prime}} \ {1}\end{array}\right]=\left[\begin{array}{lll}{a} & {b} & {c} \ {d} & {e} & {f}\end{array}\right]\left[\begin{array}{l}{x} \ {y} \ {1}\end{array}\right]
$$
所以,仿射变换的变换矩阵统一用 $\left[\begin{array}{lll}{a} & {b} & {c} \ {d} & {e} & {f}\end{array}\right]$ 来描述,不同基础变换的 $a, b, c, d, e, f$ 约束不同,如下所示:
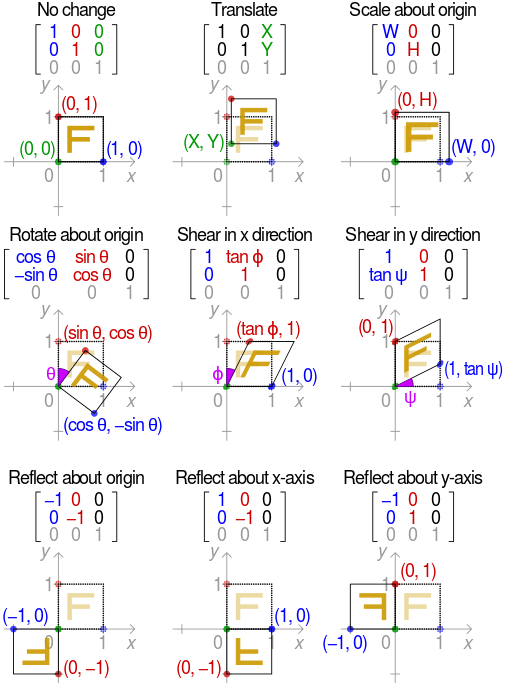
透视变换
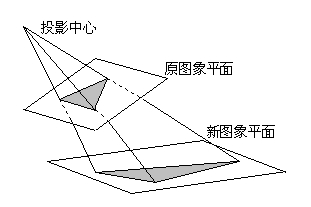
仿射变换与透视变换
仿射变换:保证物体形状的“平直性”和“平行性”
透视变换:不能保证物体形状的“平行性”