形式语言
概述
乔姆斯基(Noam Chomsky)曾经把语言定义为:按照一定规律构成的句子和符号串的有限或无限的集合。
一般地,描述一种语言可以有三种途径 [刘颖,2002;石青云 (译),1987]:
- 穷举法:把语言中的所有句子都枚举出来。显然,这种方法只适合句子数目有限的语言。
- 文法(产生式系统)描述:语言中的每个句子用严格定义的规则来构造,利用规则生成语言中合法的句子。
- 自动机法:通过对输入的句子进行合法性检验,区别哪些是语言中的句子,哪些不是语言中的句子。
文法用来精确地描述语言和其结构,自动机则是用来机械地刻画对输入字符串的识别过程。用文法来定义语言的优点是:由文法给予语言中的句子以结构,各成分之间的结构关系清楚、明了。但是,如果要直接用这些规则来确定一个字符串是否属于这套规则所定义的语言似乎并不十分明确。而由自动机来识别一个字符串是否属于该语言则相对简单,但自动机很难描述语言的结构。所以自然语言处理中的识别和分析算法,大多兼取两者之长。
形式语法的定义
形式语言是用来精确地描述语言(包括人工语言和自然语言)及其结构的手段。形式语言学也称代数语言学。
形式语法是一个4元组 $G=(N, \Sigma, P, S)$,其中 $N$ 是非终结符的有限集合(有时也叫变量集或句法种类集);$\Sigma$ 是终结符的有限集合,$N \cap \Sigma = \emptyset$;$V = N \cup \Sigma$ 称总词汇表;$P$ 是一组重写规则的有限集合:$P={ \alpha \rightarrow \beta }$,其中,$\alpha, \beta$ 是 $V$ 中元素构成的串,但 $\alpha$ 中至少应含有一个非终结符号;$S \in N$,称为句子符或初始符。
- 如果每步推导中只改写最左边的那个非终结符,这种推导称为“最左推导”。
- 如果每次都只改写最右边的非终结符,则为最右推导。__最右推导又称规范推导__。
形式语法的类型
正则文法
如果文法 $G=(N, \Sigma, P, S)$ 的 $P$ 中的规则满足如下形式:$A \rightarrow Bx$,或 $A \rightarrow x$,其中$A, B \in N, x \in \Sigma$,则称该文法为正则文法或称 3 型文法。(左线性正则文法)
如果 $A \rightarrow x B$,则该文法称为右线性正则文法。
上下文无关文法(context-free grammar, CFG)
如果 $P$ 中的规则满足如下形式:$A \rightarrow \alpha$,其中 $A \in N,\alpha \in (N \cup \Sigma)*$,则称该文法为上下文无关文法(CFG)或称 2 型文法。
上下文有关文法(context-sensitive grammar, CSG)
如果 $P$ 中的规则满足如下形式:$\alpha A \beta \rightarrow \alpha \gamma \beta$, 其中 $A \in N, \alpha, \beta, \gamma \in (N \cup \Sigma)*$,且 $\gamma$ 至少包含一个字符,则称该文法为上下文有关文法(CSG)或称 1 型文法。
另一种定义:$if \ x \rightarrow y, x \in (N \cup \Sigma)+, y \in (N \cup Sigma)*$,并且 $|y| \geq |x|$。
无约束文法(无限制重写系统)
如果 $P$ 中的规则满足如下形式:$\alpha \rightarrow \beta$,$\alpha, \beta$ 是字符串,则称 $G$ 为无约束文法,或称 0 型文法。
显然,每一个正则文法都是上下文无关文法,每一个上下无关文法都是上下文有关文法,而每一个上下文有关文法都是 0 型文法,即:$L(G3) \subseteq L(G2) \subseteq L(G1) \subseteq L(G0)$。
语言与文法类型的约定
如果一种语言能由几种文法所产生,则把这种语言称为在这几种文法中受限制最多的那种文法所产生的语言。
CFG 识别句子的派生树表示


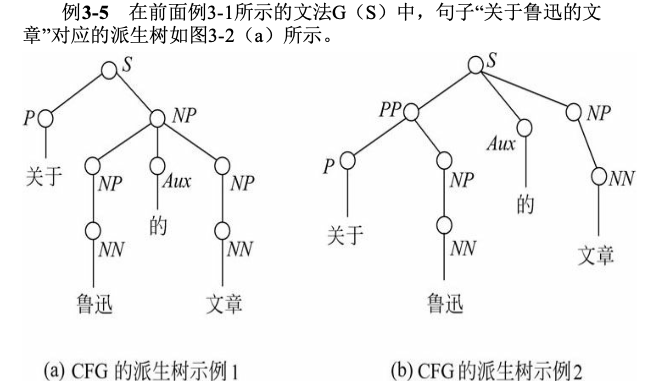
一个文法 $G$,如果存在某个句子有不只一棵分析树与之对应,那么称这个文法是二义的。
自动机理论
有限自动机
有限自动机又分为确定性有限自动机(definite automata, DFA)和不确定性有限自动机(non-definite automata, NFA)两种。
确定的有限自动机(definite automata, DFA)
确定的有限自动机 $M$ 是一个五元组:$M = (\Sigma, Q, \delta, q_0, F)$
- $\Sigma$ 是输入符号的有穷集合;
- $Q$ 是状态的有限集合;
- $q_0 \in Q$ 是初始状态;
- $F$ 是终止状态集合,$F \subseteq Q$;
- $\delta$ 是 $Q$ 与 $\Sigma$ 的直积 $Q×\Sigma$ 到 $Q$ (下一个状态)的映射。它支配着有限状态控制的行为,有时也称为状态转移函数。
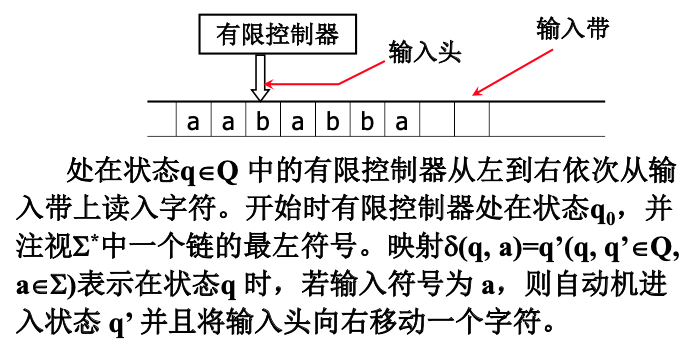
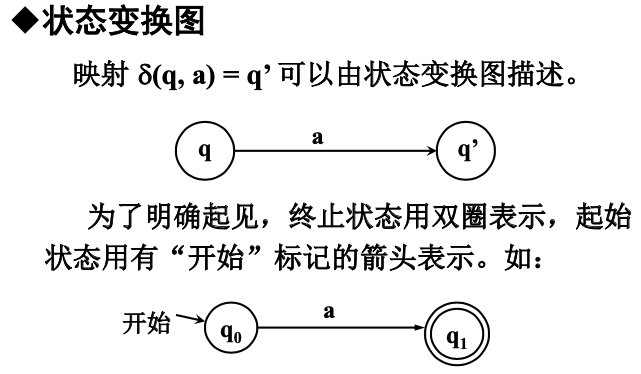
DFA 定义的语言
如果一个句子 $x$ 使得有限自动机 $M$ 有 $\delta(q_0, x) = p, p \in F$,那么,称句子 $x$ 被 $M$ 接受。由 $M$ 定义的语言 $T(M)$ 就是被 $M$ 接受的句子的全集。即:$T(M) = {x | \delta(q_0, x) \in F }$
不确定的有限自动机(non-definite automata, NFA)
不确定的有限自动机 $M$ 是一个五元组 $M = (\Sigma, Q, \delta, q_0, F)$
- $\Sigma$ 是输入符号的有穷集合;
- $Q$ 是状态的有限集合;
- $q_0 \in Q$ 是初始状态;
- $F$ 是终止状态集合,$F \subseteq Q$;
- $\delta$ 是 $Q$ 与 $\Sigma$ 的直积 $Q×\Sigma$ 到Q的幂集 $2^Q$ 的映射。
NFA 与 DFA 的关系和区别
NFA 与 DFA 的唯一区别是:在 NFA 中 $\delta(q, a)$ 是一个状态集合,而在 DFA 中 $\delta(q, a)$ 是一个状态。
设 $L$ 是一个被 NFA 所接受的句子的集合,则存在一个 DFA,它能够接受 $L$。
正则文法与有限自动机的关系
若 $G = (V_N, V_T, P, S )$ 是一个正则文法,则存在一个有限自动机 $M=(\Sigma, Q, \delta, q_0, F)$,使得: $T(M) = L(G)$。
由 $G$ 构造 $M$ 的一般步骤:
- 令 $\Sigma =V_T, Q=V_N \cup {T}, q_0=S$,其中,$T$ 是一个新增加的非终结符。
- 如果在 $P$ 中有产生式 $S \rightarrow \epsilon$,则 $F={S, T}$,否则 $F={T}$。
- 如果在 $P$ 中有产生式 $B \rightarrow a, B \in V_N, a \in V_T$,则 $T \in \delta(B, a)$。
- 如果在 $P$ 中有产生式 $B \rightarrow aC, B, C\in V_N,a \in V_T$,则 $C \in \delta(B, a)$。
- 对于每一个 $a \in V_T$,有 $\delta(T, a) = \emptyset$。
若 $M=(\Sigma, Q, \delta, q_0, F$ 是一有限自动机,则存在正则文法 $G = (V_N, V_T, P, S )$ 使 $L(G)=T(M)$。
由 $M$ 构造 $G$ 的一般步骤:
- 令 $V_N = Q, V_T = \Sigma, S = q_0$;
- 如果 $C \in \delta(B, a), B, C \in Q, a \in \delta$,则在 $P$ 中有产生式 $B \rightarrow aC$;
- 如果 $C \in \delta(B, a), C \in F$,则在 $P$ 中有产生式 $B \rightarrow a$。
下推自动机
下推自动机(push-down automata, PDA)
PDA 可以看成是一个带有附加的下推存储器的有限自动机,下推存储器是一个栈。
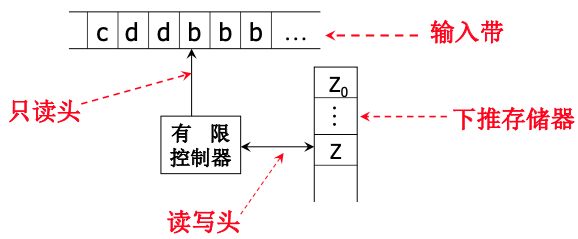
一个不确定的 PDA 可以表达成一个 7 元组:$M = (\Sigma, Q, \Gamma, \delta, q_0, Z_0, F)$
- $\Sigma$ 是输入符号的有穷集合;
- $Q$ 是状态的有限集合;
- $q_0 \in Q$ 是初始状态;
- $\Gamma$ 为下推存储器符号的有穷集合;
- $Z_0 \in \Gamma$ 为最初出现在下推存储器顶端的符号;
- $F$ 是终止状态集合,$F \subseteq Q$;
- $\delta$ 是从 $Q×(\Sigma \cup {\epsilon})×\Gamma$ 到 $Q×\Gamma*$ 子集的映射。
映射关系 $\delta$ 的解释
映射关系 $\delta(q, a, Z)={(q_1, \gamma_1), (q_2, \gamma_2),…,(q_m, \gamma_m)}$
其中, $q_1, q_2, …, q_m \in Q, a \in \Sigma, Z \in \Gamma, \gamma_1, \gamma_2,…,\gamma_m \in \Gamma*$。
该映射的意思是:当 PDA 处于状态 $q$,面临输入符号 $a$ 时,自动机将进入 $q_i, i = 1, 2, …, m$ 状态,并以 $\gamma_i$ 来代替下推存储器(栈)顶端符号 $Z$,同时将输入头指向下一个字符。当 $Z$ 被 $\gamma_i$ 取代时,$\gamma_i$ 的符号按照从左到右的顺序依次从下向上推入到存储器。
特殊情况下,当 $\delta(q, a, Z)={(q_1, \gamma_1), (q_2, \gamma_2),…,(q_m, \gamma_m)}$ 时,输入头位置不移动,只用于处理下推存储器内部的操作,叫作“$\epsilon$ 移动”。
另外两种自动机
图灵机
- 图灵机与 0 型文法等价;
- 图灵机与有限自动机(FA)的区别:图灵机可以通过其读/写头改变输入带的字符。
线性带限自动机
- 线性带限自动机与 1 型文法等价;
- 线性带限自动机是一个确定的单带图灵机,其读写头不能超越原输入带上字符串的初始和终止位置,即线性带限自动机的存储空间被输入符号串的长度所限制。
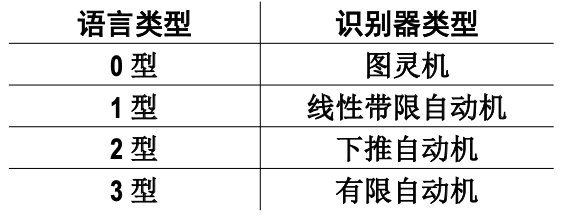
语言与识别器的对应关系