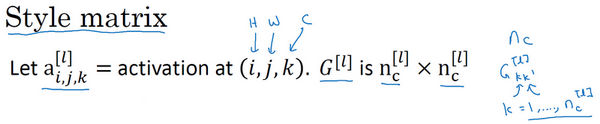$J_{\text{content}}(C,G)$
第一部分被称作内容代价,这是一个关于内容图片和生成图片的函数,它是用来度量生成图片$G$的内容与内容图片$C$的内容有多相似。
$J_{\text{style}}(S,G)$
然后我们会把结果加上一个风格代价函数,也就是关于$S$和$G$的函数,用来度量图片$G$的风格和图片$S$的风格的相似度。
$J( G) = a J_{\text{content}}( C,G) + \beta J_{\text{style}}(S,G)$
内容代价函数(Content cost function)

假如说,你用隐含层$l$来计算内容代价,如果$l$是个很小的数,比如用隐含层1,这个代价函数就会使你的生成图片像素上非常接近你的内容图片。然而如果你用很深的层,那么那就会问,内容图片里是否有狗,然后它就会确保生成图片里有一个狗。所以在实际中,这个层$l$在网络中既不会选的太浅也不会选的太深。因为你要自己做这周结束的编程练习,我会让你获得一些直觉,在编程练习中的具体例子里通常$l$会选择在网络的中间层,既不太浅也不很深,然后用一个预训练的卷积模型,可以是VGG网络或者其他的网络也可以。

现在你需要衡量假如有一个内容图片和一个生成图片他们在内容上的相似度,我们令这个$a^{[l][C]}$和$a^{[l][G]}$,代表这两个图片$C$和$G$的$l$层的激活函数值。如果这两个激活值相似,那么就意味着两个图片的内容相似。
$J_{\text{content}}( C,G) = \frac{1}{2}|| a^{[l][C]} - a^{[l][G]}||^{2}$
为两个激活值不同或者相似的程度,我们取$l$层的隐含单元的激活值,按元素相减,内容图片的激活值与生成图片相比较,然后取平方,也可以在前面加上归一化或者不加,比如$\frac{1}{2}$或者其他的,都影响不大,因为这都可以由这个超参数$a$来调整($J(G) =a J_{\text{content}}( C,G) + \beta J_{\text{style}}(S,G)$)
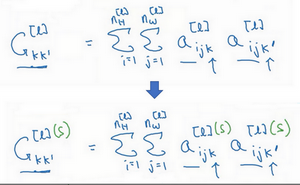
风格代价函数(Style cost function)