熵又称为自信息(self-information),表示信源 X 每发一个符号(不论发什么符号)所提供的平均信息量。__熵也可以被视为描述一个随机变量的不确定性的数量。一个随机变量的熵越大,它的不确定性越大。那么,正确估计其值的可能性就越小__。越不确定的随机变量越需要大的信息量用以确定其值。
转自:https://www.zhihu.com/question/22178202/answer/49929786
信息熵,信息熵,怎么看怎么觉得这个“熵”字不顺眼,那就先不看。我们起码知道这个概念跟信息有关系。而它又是个数学模型里面的概念,一般而言是可以量化的。所以,第一个问题来了:信息是不是可以量化?
起码直觉上而言是可以的,不然怎么可能我们觉得有些人说的废话特别多,“没什么信息量”,有些人一语中的,一句话就传达了很大的信息量。
为什么有的信息量大有的信息量小?
有些事情本来不是很确定,例如明天股票是涨还是跌。如果你告诉我明天NBA决赛开始了,这两者似乎没啥关系啊,所以你的信息对明天股票是涨是跌带来的信息量很少。但是假如NBA决赛一开始,大家都不关注股票了没人坐庄股票有99%的概率会跌,那你这句话信息量就很大,因为本来不确定的事情变得十分确定。
而有些事情本来就很确定了,例如太阳从东边升起,你再告诉我一百遍太阳从东边升起,你的话还是丝毫没有信息量的,因为这事情不能更确定了。
所以说信息量的大小跟事情不确定性的变化有关。
那么,不确定性的变化跟什么有关呢?
- 跟事情的可能结果的数量有关;
- 跟概率有关。
先说一。例如我们讨论太阳从哪升起。本来就只有一个结果,我们早就知道,那么无论谁传递任何信息都是没有信息量的。
当可能结果数量比较大时,我们得到的新信息才有潜力拥有大信息量。
二,单看可能结果数量不够,还要看初始的概率分布。例如一开始我就知道小明在电影院的有15*15个座位的A厅看电影。小明可以坐的位置有225个,可能结果数量算多了。可是假如我们一开始就知道小明坐在第一排的最左边的可能是99%,坐其它位置的可能性微乎其微,那么在大多数情况下,你再告诉我小明的什么信息也没有多大用,因为我们几乎确定小明坐第一排的最左边了。
那么,怎么衡量不确定性的变化的大小呢?怎么定义呢?
这个问题不好回答,但是假设我们已经知道这个量已经存在了,不妨就叫做信息量,那么你觉得 信息量起码该满足些什么特点呢?
- __起码不是个负数吧__,不然说句话还偷走信息呢~
- __起码信息量和信息量之间可以相加吧__!假如你告诉我的第一句话的信息量是3,在第一句话的基础上又告诉我一句话,额外信息量是4,那么两句话信息量加起来应该等于7吧!难道还能是5是9?
- 刚刚已经提过,信息量跟概率有关系,但我们应该会觉得,信息量是连续依赖于概率 的吧!就是说,某一个概率变化了 0.0000001,那么这个信息量不应该变化很大。
- 刚刚也提过,信息量大小跟可能结果数量有关。__假如每一个可能的结果出现的概率一样,那么对于可能结果数量多的那个事件,新信息有更大的潜力具有更大的信息量__,因为初始状态下不确定性更大。
那有什么函数能满足上面四个条件呢?负的对数函数,也就是 $-log(x)$!底数取大于 1 的数保证这个函数是非负的就行。前面再随便乘个正常数也行。
- 为什么不是正的?因为假如是正的,由于 x 是小于等于 1 的数,$log(x)$ 就小于等于 0 了。第一个特点满足。
- 咱们再来验证一下其他特点。三是最容易的。假如 x 是一个概率,那么 $log(x)$ 是连续依赖于 x 的。
- 四呢?假如有 n 个可能结果,那么出现任意一个的概率是 1/n,而 $-log(1/n)$ 是 n 的增函数,没问题。
- 最后验证二。由于 $-log(xy) = -log(x) -log(y)$,所以也是对的。学数学的同学注意,这里的 y 可以是给定 x 的条件概率,当然也可以独立于 x。
By the way,这个函数是唯一的(除了还可以多乘上任意一个常数),有时间可以自己证明一下,或者查书。
ok,所以我们知道一个 __事件的信息量就是这个事件发生的概率的负对数__。
最后终于能回到信息熵。信息熵是跟所有可能性有关系的。每个可能事件的发生都有个概率。__信息熵就是平均而言发生一个事件我们得到的信息量大小。所以数学上,信息熵其实是信息量的期望__。
$H=-\sum_{x \in U} P(x) \log P(x)$
至于为什么用“熵”这个怪字?大概是当时翻译的人觉得这个量跟热力学的熵有关系,所以就用了这个字,君不见字里头的火字旁?而热力学为什么用这个字?这个真心不知道。。。
据评论里 @林杰威 的说法:熵最早是由热力学定义的一个函数,是普朗克来中国讲学的时候引入的。英文是“entropy”这个字,中文词汇中没有相关的字眼。当时是一个有名的姓胡的学者作为普朗克的翻译。因为这个熵“S”是定义为热量Q与温度的比值,所以当时他翻译是立刻创造出熵这个字,从火,从商。
联合熵(joint entropy)
如果 X, Y 是一对离散型随机变量 $X, Y \sim p(x, y)$, X, Y 的联合熵 $H(X, Y)$ 为:
$$
H(X, Y)=-\sum_{x \in X} \sum_{y \in Y} p(x, y) \log _{2} p(x, y)
$$
联合熵实际上就是描述一对随机变量平均所需要的信息量。
条件熵(conditional entropy)
给定随机变量 X 的情况下,随机变量 Y 的条件熵定义为:
$$
\begin{aligned}
H(Y | X) &=\sum_{x \in X} p(x) H(Y | X=x) \
&=\sum_{x \in X} p(x)\left[-\sum_{y \in Y} p(y | x) \log {2} p(y | x)\right] \
&=-\sum{x \in X} \sum_{y \in Y} p(x, y) \log _{2} p(y | x)
\end{aligned}
$$
联合熵、条件熵的关系
$\begin{aligned} H(X, Y) &=-\sum_{x \in X} \sum_{y \in Y} p(x, y) \log [p(x) p(y | x)] \ &=-\sum_{x \in X} \sum_{y \in Y} p(x, y)[\log p(x)+\log p(y | x)] \ &=-\sum_{x \in X} \sum_{y \in Y} p(x, y) \log p(x)-\sum_{x \in X} \sum_{y \in Y} p(x, y) \log p(y | x) \ &=-\sum_{x \in X} p(x) \log p(x)-\sum_{x \in X} \sum_{y \in Y} p(x, y) \log p(y | x) \ &=H(X)+H(Y | X)\end{aligned}$
熵率
一般地,对于一条长度为 n 的信息,每一个字符或字的熵为:
$$
H_{\text {rate }}=\frac{1}{n} H\left(X_{\text {ln }}\right)=-\frac{1}{n} \sum_{x_{\text {1n }}} p\left(x_{\text {ln }}\right) \log p\left(x_{\text {1n }}\right)
$$
这个数值我们也称为熵率(entropy rate)。其中,变量 $X_{1n}$ 表示随机变量序列 $(X_1, …, X_n)$,$x_{1n} = (x_1, …, x_n)$ 表示随机变量的具体取值。有时将 $x_{1n}$ 写成:$x_1^n$。
相对熵(relative entropy)
相对熵(relative entropy, 或称 Kullback-Leibler divergence, KL 距离)
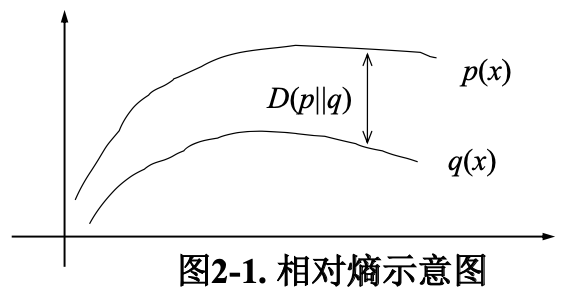
两个概率分布 $p(x)$ 和 $q(x)$ 的相对熵定义为:
$$
D(p | q)=\sum_{x \in X} p(x) \log \frac{p(x)}{q(x)}
$$
该定义中约定 $0 log (0/q) = 0$,$p log (p/0) = \infty$。
相对熵常被用以衡量两个随机分布的差距。当两个随机分布相同时,其相对熵为 0。当两个随机分布的差别增加时,其相对熵也增加。
交叉熵(cross entropy)
如果一个随机变量 $X \sim p(x)$,$q(x)$ 为用于近似 $p(x)$ 的概率分布,那么,随机变量 $X$ 和模型 $q$ 之间的交叉熵定义为:
$$
\begin{aligned}
H(X, q) &=H(X)+D(p | q) \
&=-\sum_{x} p(x) \log q(x)
\end{aligned}
$$
交叉熵的概念用以衡量估计模型与真实概率分布之间的差异。
对于语言 $L=(X) \sim p(x)$ 与其模型 $q$ 的交叉熵定义为:
$$
H(L, q)=-\lim {n \rightarrow \infty} \frac{1}{n} \sum{x_{1}^{n}} p\left(x_{1}^{n}\right) \log q\left(x_{1}^{n}\right)
$$
其中,
- $x^n_1=x_1,…,x_n$ 为语言L的词序列(样本);
- $p(x_1^n)$ 为 $x_1^n$ 的概率(理论值);
- $q(x_1^n)$ 为模型 $q$ 对 $x_1^n$ 的概率估计值。
信息论中有如下定理:假定语言 L 是稳态(stationary)遍历性(ergodic)随机过程,$x^n_1$ 为 L 的样本,那么,有:
$$
H(L, q)=-\lim {n \rightarrow \infty} \frac{1}{n} \log q\left(x{1}^{n}\right)
$$
由此,我们可以根据模型 $q$ 和一个含有大量数据 的 $L$ 的样本来计算交叉熵。__在设计模型 $q$ 时,我们的目的是使交叉熵最小,从而使模型最接近真实的概率分布 $p(x)$__。
相对熵与交叉熵
由于 $H(X, q) =H(X)+D(p | q)$。机器学习的目的就是希望 $q(x)$ 尽可能地逼近甚至等于 $p(x)$,从而使得相对熵接近最小值 0。由于真实的概率分布是固定的,相对熵公式的前半部分 $H(X)$ 就成了一个常数。那么相对熵达到最小值的时候,也意味着交叉熵达到了最小值。对 $q(x)$ 的优化就等效于求交叉熵的最小值。另外,对交叉熵求最小值,也等效于求最大似然估计(maximum likelihood estimation)。
困惑度(perplexity)
在设计语言模型时,我们通常用困惑度来代替交叉熵衡量语言模型的好坏。给定语言 $L$ 的样本 $l_1^n = l_1 … l_n$,$L$ 的困惑度 $PP_q$定义为:
$$
P P_{q}=2^{H(L, q)} \approx 2^{-\frac{1}{n} \log q\left(l_{1}^{n}\right)}=\left[q\left(l_{1}^{n}\right)\right]^{-\frac{1}{n}}
$$
语言模型设计的任务就是寻找困惑度最小的模型,使其最接近真实的语言。
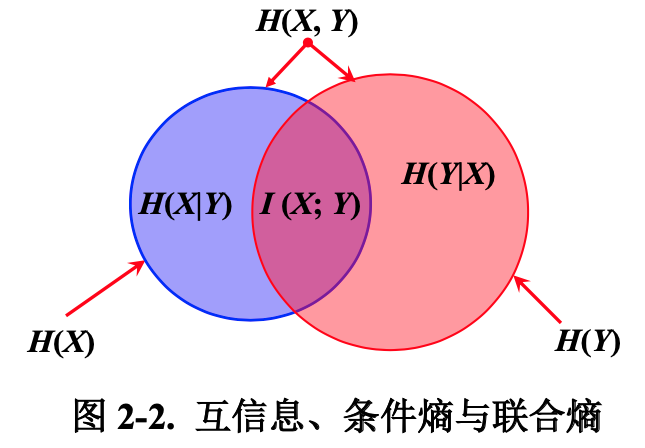
如果 $(X, Y) \sim p(x, y)$,$X, Y$ 之间的互信息 $I(X; Y)$ 定义为:
$$
I(X; Y) = H(X) - H(Y|X)
$$
根据 $H(X)$ 和 H(X|Y)$ 的定义:
- $H(X)=-\sum_{x \in X} p(x) \log _{2} p(x)$
- $H(X | Y)=-\sum_{x \in X} \sum_{y \in Y} p(x, y) \log _{2} p(x | y)$
$$
\begin{aligned}
I(X ; Y) &=H(X)-H(X | Y) \
&=-\sum_{x \in X} p(x) \log {2} p(x)+\sum{x \in X} \sum_{y \in Y} p(x, y) \log {2} p(x | y) \
&=\sum{x \in X} \sum_{y \in Y} p(x, y)\left(\log {2} p(x | y)-\log {2} p(x)\right) \
&=\sum{x \in X} \sum{y \in Y} p(x, y)\left(\log {2} \frac{p(x | y)}{p(x)}\right) \
I(X ; Y) &=\sum{x \in X} \sum_{y \in Y} p(x, y) \log _{2} \frac{p(x, y)}{p(x) p(y)}
\end{aligned}
$$
互信息 $I (X; Y)$ 是在知道了 $Y$ 的值以后 $$ 的不确定性的减少量,即 $Y$ 的值透露了多少关于 $X$ 的信息量。
注:类似决策树中的信息增益。
互信息值越大,表示两个汉字之间的结合越紧密,越可能成词。反之,断开的可能性越大。
当两个汉字 $x$ 和 $y$ 关联度较强时,其互信息值 $I(x, y)>0$;$x$ 与$y$ 关系弱时,$I(x, y)≈0$;而当 $I(x, y)<0$ 时,$x$ 与 $y$ 称为 “互补分布”。
在汉语分词研究中,有学者用双字耦合度的概念代替互信息:设 $c_i$,$c_{i+1}$ 是两个连续出现的汉字,统计样本中 $c_i$,$c_{i+1}$ 连续出现在一个词中的次数和连续出现的总次数, 二者之比就是 $c_i$,$c_{i+1}$ 的双字耦合度:
$\text { Couple }\left(c_{i}, c_{i+1}\right)=\frac{N\left(c_{i} c_{i+1}\right)}{N\left(c_{i} c_{i+1}\right)+N\left(\cdots c_{i} | c_{i+1} \cdots\right)}$
- $N(c_i c_{i+1})$ 表示字符串$c_i c_{i+1}$构成的词出现的频率
- $N(…c_i|c_{i+1}…)$ 表示 $c_i$ 作为上一个词的词尾且 $c_{i+1}$ 作为相邻下一个词的词头出现的频率
注意:此处“|”不表示条件概率!